blahdy
James joined
If it flies, it dies™.
Understanding Physics Scaling in World in Conflict
WiC MW Mod portrays combat in around 20-30km of effective front line battlespace for application of most tactical weapons. Weapons of more strategic assets (such as ballistic missiles and cruise missiles) make certain geometry compromises to fictionally portray them in such a small battle space.
FLINT (Flexible Interceptor) is the code base and common source library written in Python which provides much of the physics and guidance algorithms for agents acting as projectiles in game. Agents in game using the FLINT system have completely replaced WiC's HomingShooter and BallisticShooter projectile types altogether.
The problem of small maps
Maps in World in Conflict are statically limited to a square of 1.5km by 1.5km (2.25km^2). Every map is the same size at 2.25km^2 regardless of how the map creator wishes to size his map. Smaller maps are possible by simply disabling play field, but the size of the map remains at 2.25km^2. While EX3D World could address larger coordinate space (10km by 10km is tested so far) to potentially enable future addition of off-map assets, the small playfield of 2.25km^2 that is usable by players severely limits the application of any modern combat systems.
The goal of the MW Mod isn't to simulate realism, but instead, provide an "authentic" combat system experience in a fun arcade setting, where any casual player would enjoy authentic portrayal of modern weapon systems, without expectation of perfect realism or excessive complexity. In order to meet this authenticity in player experience, various physics properties will have to be scaled down fictionally, in order to provide the additional battlespace as required by MW Mod.
Distance (range scale down)
Unit-to-unit separation distance in FLINT is scaled by a factor of 10. For example, 100 meters would equate to 1 kilometer in game; thus, 1500m by 1500m map is now 15km by 15km. Altitude is also scaled down at the same factor by 10. 350 meters altitude height would equate to 3.5km or 11482 ft.
Even with scale down by a factor of 10, weapon systems will have to be range limited for balancing reasons. For example, while Hellfire missile in game kinematically could hit targets out to ~7-9km (depending on trajectory shaping), its firing range is limited to 4.5km by shooter's launch inhibit setting. Of course, players can often cheat range limits by using laser-guided Hellfire (not Longbow) and firing the missile at a blank terrain out to 4.5km as maximally allowed, then extending its range in flight by lasing a further away target with JTAC infantry. Kill distances of up to ~7.5km was reported by players using this method.
Velocity, movement speed, etc.
Unfortunately, simply scaling everything down by a factor of 10 does not work in practice. Everything will look ridiculously small to the point of ruining the game experience. For example, consider that speed of sound (1.0 Mach) in SI meters is ~343m/s. Scaling this down by 10 would mean 34.3m/s, which is roughly about the speed of a scout helicopter in vanilla WiC -- you see what I'm getting at here: everything is going to be so slow and look awfully stupid. Thus, speed-of-sound in FLINT is 60 meters/second, which represents downscale factor of 5.72 times.
Not everything can be scaled down as well. We don't want to make tanks and vehicles move 10 times slower, so vehicles generally move at 8-9 meters/second. When comparing this to the FLINT referenced speed of sound, this means vehicles are effectively moving at 185km/h, which is an impossibly insane speed for a tank, but we choose to ignore the same scale restrictions on unit movements for playability purposes. Having said that, no player usable unit (except for jets) will ever move faster than 28 meters/second in FLINT physics scale -- no user controlled agents may ever reach velocity faster than half of simulated speed of sound, in order to maintain an intricate balance of game playability vs. experience & feel.
Gravity
Gravity is inversely proportional to the square of the distance from earth. However, gravitational acceleration (1G) in FLINT is capped at approximately 8.75m/s/s. This means
that for up to about 372km altitude, gravity is constant at 8.75m/s/s in FLINT's reference scale -- gravity effect will be the same for an object regardless of whether it is 40km high or sitting on ground level. Above 372km altitude (for IRBMs, SM-3, etc), FLINT proportionally decreases gravitational acceleration inversely with increasing distance.
Dynamic Pressure
Calculation of Dyn Q in FLINT uses real world SI units and US Standard Atmosphere model -- we actually want aerodynamic forces to affect projectiles faster in our small battlespace, so we chose not to scale things down here. This means at roughly around 32-40km altitude, dynamic pressure will practically become close to zero. Currently, only PAC-3 MSE and ballistic missiles can reach this level of 'drag-free' altitude (SM-6, which is under development, is also expected to reach near this altitude at around 31-33km peak height). How the re-entry physics and drag forces will work at even higher altitudes (above 86km) is an ongoing area of study and research for future developments.
Because Dyn Q is computed at real world SI units and atmosphere model, while everything else is scaled down, this does create some interesting observations (though does not ruin the game experience). One of which is excessive G load placed on agents after cessation of thrust whilst under high pressure. While it is normal for rockets to momentarily experience high G load after motor burn out at low altitudes where atmosphere is thick, in FLINT, this effect is more pronounced. It's possible for AIM-120 in game to pull 14 G's at peak simply by the blunt force of atmospheric pressure at lower altitudes after motor burnout. Not an issue from gameplay or authenticity perspectives -- this is simply an observation of having projectiles affected by drag faster in WiC's small world size, compared to other units of measure being scaled down.
Issue of Barometric Altitude
While simulation of Dynamic Pressure substantially improves authenticity and realism feel of rockets in motion, a critical caveat is the issue of reference for the actual altitude in game.
Dynamic pressure is dependent upon barometric altitude from mean sea level. However, FLINT currently does not use barometric altitude, but uses ground-referenced altitude, which is not correct. This means, having excessively high mountains in the game map will have little effect on increasing launch performance of the rocket, as the point of barometric pressure reference is incorrectly made from ground level, not from sea level. But, if the rocket launches at the edge of a tall cliff, it would immediately gain from the altitude benefit, as it would be flying higher once it clears the cliff's edge.
Because of this, the only way rockets could surely benefit from high altitude in game today, is by being launched from aircraft, not from tall terrains. Not really a big issue right now, as you'd have to have a pretty tall mountain to provide a measurable benefit for rocket's aerodynamic performance on launch.
This however creates some minor problems in physics with respect to projectiles in motion. For example, objects in free fall will continuously accelerate until increasing atmospheric pressure cancels out the gravitational acceleration -- when this is achieved, it is said that the object has reached "terminal velocity".
Once terminal velocity is achieved, unless the object changes its drag profile while falling (such as breaking apart or deploying a parachute), object will continue falling down at constant velocity which is at an equilibrium of gravitational acceleration vs. increasing atmospheric density. Because of the lack of barometric altitude reference by FLINT, dynamic pressure will change slightly as object traverses over different terrain profiles -- this will make deviations in drag force, where terminal velocity in FLINT is only approximately constant and deviates as the object moves over different terrain heights.
We're looking to fix this caveat and introduce barometric altitude in future versions of the mod, though it isn't really high on the priority list. It is currently an area of research and test with respect to the game itself -- the main issue is that every map uses different water table level in WiC; it is entirely up to the map creator to determine at what height water table will appear in WiCEd tool. So, we will have to find a clean way to load each map's .Ice parasites to find the water table level, or estimate a best guess average of the mean sea level across commonly played maps.
Missile Orientation Rendering
FLINT 7 introduces 3x3 rotation matrix to compute object orientation, which is then converted to yaw and pitch angles to be rendered in game. Unfortunately, WiC CopterMover does not provide a mechanism to alter roll orientation, so the computed roll angle is ignored and not rendered (though this may change in the future via a crude hack).
The introduction of rotation matrix allows orientation rendering from the object's local frame of reference, which is then converted to world space for EX3D rendering. One of the key benefits of moving to the new rotation based rendering is that it allows us to easily render angle-of-attack (AoA) orientation of the missile. Quaternion rotation is under development for the Next Generation EXFLINT Renderer (NGEX), where a single quaternion will replace yaw, pitch and roll computations entirely.
This new method of rendering object orientation finally solves the difficult "vertical launch orientation" problems we've had in the past. This was one of the most annoying holy grail issues during MW Mod development, where vertically launching missiles such as Tor M1 and S-300 were very difficult to orient properly in the game. This was one of the major stumbling blocks that prevented naval unit developments for a while, as missiles are vertically launched from the ship's VLS. You may notice that S-300 and Tor M1 missiles now look beautifully realistic and work flawlessly in FLINT 7 (MW Mod 6 development) videos, compared to older versions -- this is the result of the new orientation rendering.
Angle of Attack (AoA) and Induced Drag
As missile flies higher, atmospheric pressure goes down with increasing altitude. However, the weight force on the missile does not change (actually fuel consumption does lower weight, but let's call that negligible for the purpose of this discussion). With decreasing lift, the missile is continually being pressed down by gravity and guidance system has to work harder to keep the missile flying in the air -- thus, more lift force is required to overcome the force of gravity. To aid in this, missile's angle of attack is increased to generate more lift by forcibly inducing more drag -- you may notice that cruise missiles flying at higher altitudes in game are pointing their nose up by a few degrees to increase the generated lift and help stay afloat in the air.
Looking back in time..
Since the early experiment known as "Flexible, Advanced Air Interceptor Missile Script" (later simplified to "Flexible Interceptor", shortened as 'FLINT') during early days of World in Conflict modding back in 2010, MW Mod development has come a long way in changing the way modern combat systems are portrayed in World in Conflict. Proportional Navigation (PN) theory was understood and implemented for the first time in July 2011, resulting in a major breakthrough in homing missile development for World in Conflict.
The implementation of PN in FLINT was inspiring to say at least, and it's awesome to see that more games and mods are implementing PN as their preferred choice for lead-pursuit homing missiles as well. We're looking forward to collaborating more and will begin pushing more code samples at our Github page (Github.com)
Another aspect of important recent development is the launch of Massgate.org, a community run Massgate service for World in Conflict, which was made possible by Nukem's decoding of the Massgate protocol infrastructure. This also resulted in an extremely positive development for MW Mod as well, especially in debugging new features.
After the Massgate.org implementation, EX-WCC (EX World Weapons Control Computer) runtime environment was also developed, to unify all complex air and missile defense complexes in game under a single program entity. The EX-WCC has a stack machine interpreter for basic tasks, a process scheduler and a dispatcher, and simulates execution environment using POSIX standard model. Using the EX-WCC virtual machine, several different elements in the game (e.g. Aegis, Patriot/IBCS, surface fires, etc) are all able to work together in a cooperative fashion.
Moving forward..
We're planning to deliver MW Mod 6.0 Release this year, with first implementation of naval asset on BLUEFOR side, and corresponding coastal anti-ship/maritime strike capability on REDFOR side, along with lot of improvements made to ground combat elements. As of now, MW Mod 6.0 development is about 65% complete; only major work that is left is complete rewrite of 3M55 Oniks (SS-N-26 Strobile) supersonic cruise missile for REDFOR side. We're not sure if SM-6 will make it to 6.0 release, it may or, may end up being pushed to post-6.0 release, but we shall see.
State of World in Conflict MW Mod
May, 2019 marks the 10th year anniversary of what was once called Fun Mod for World in Conflict (later renamed to MW Mod around 2010 during beta development). In 10 years of modding World in Conflict, MW Mod had come a long way since its nascent years.
Some of the biggest achievements during MW Mod’s 10 years include:
- Integrated Air and Missile Defense System (IAMD) and its continued development and successes over the years.
- Complete redo of infantry role and introduction of team artillery fire support channel (JFSN) and Joint Terminal Attack Controller (JTAC), maximizing infantry-air and infantry-support coordination. JTAC infantry guiding GBUs & Hellfire missiles and airborne infantry calling artillery are just wicked cool.
- Flexible Interceptor (FLINT) missile & projectile simulation system: The crown jewel of MW Mod development. What initially started as a silly experiment to improve homing missiles had ended up practically replacing the whole game.
Is there a new version coming out?
Yes! To celebrate the 10-year anniversary of MW Mod, we’re currently working on the next release (version 5.5), known as “Starscream” for development name. We’re introducing the following new features and units to Starscream/5.5:
- Counter-Battery Radar for BLUEFOR (dropped via TA):
This is a feature many people wanted since vanilla WiC’s release in 2007 to make for fun artillery duels. 12 years later and we finally have it, and this is one hell of an over-engineered and wicked cool unit.
Counterfire radar will track incoming rocket, artillery & mortar (RAM) threats and alert friendly units of incoming artillery attack at the estimated impact area (early warning function). The radar performs backtracking calculations on RAM trajectories and will attempt to trace the weapon firing location. Once traced, radar will reveal the weapon firing source and automatically request counterfire mission from support’s Networked Artillery (MLRS) units via team fire support channel (JFSN).
The Integrated Air & Missile Defense System (IAMD) in WiC MW Mod has now evolved to following the unified IAMD Battle Command System (IBCS) model. Counterfire radar works as a “plug-in sensor” into the IBCS network. In order for the Counterfire Radar to function, your team needs to have either NATO Fire Control Radar unit or Heavy SAM (Patriot SAM site) operating somewhere in the map.
Both Patriot and Fire Control Radar units provide Command & Control (Engagement Operation Center or EOC) functions for the Counterfire Radar and all air defense related units to run in game. Without EOC units, there is no command and control.
Note that Counterfire Radars, like all radars, are subject to anti-radiation missile (ARM) attacks from REDFOR jet aircraft. Be sure to protect it with Medium SAM (IFPC MML) or airdropped C-RAM. Or passively, if you see an incoming ARM going for your radar, you can shut down the radar by placing the unit into Hold-Fire. Place the unit on Hold-Fire and move it out of the area to completely trash the incoming ARM. - Small improvements to Scripted AI:
Based on community feedback, we’ve made some small improvements to the scripted AI in game when bots are present. On supported maps, REDFOR AI will now emplace static AA and AT units (Pantsir S1, Tor M1 and Kornet-D) at strategic locations to help defend the spawn zone and prevent overruns.
Additionally, when there are no human players present in BLUEFOR side (humans stacked on RED side), then BLUEFOR support AI will now spawn and operate the Counter-Battery Radar (you may want to move your BM-21s after firing them.. lest they get obliterated by counterfire). - Truck bomb mode for REDFOR infantry transport trucks:
Another community request for rather fun laughs than a useful gameplay feature. REDFOR transport trucks can be configured into truck bomb mode by enabling Offensive Ability. - AGM-158B Joint Air-to-Surface Standoff Missile (JASSM):
Based upon community request from Facebook, we’re adding another cruise missile to the game, this time an air-launched JASSM cruise missile dropped from F-18 (CAS2) aircraft.
The weapon employment logic for JASSM will be as follows:
Human player triggered launch options:
Human players can trigger a JASSM launch from F-18 by either:
(a) designating a target with JTAC that is really far away from F-18 (on other side of the map); or
(b) launch a Tomahawk cruise missile using cruise missile launcher.
If you are attacking an enemy target of high value with Tomahawk (e.g. SAM site, artillery, missile launcher, etc), F-18 will also add its own share of fire by launching JASSM at the same location, to help saturate and brute-force through enemy air defenses.
AI launch options:
If there are no human players present on BLUEFOR side (humans stacked on RED side), scripted AI will routinely scan for enemy units that are either visible or generating emissions (e.g. radars), and will add them to strike queue for JASSM attacks.
Along with JASSM, ground-launched cruise missiles have also been improved. Mission data (flight plan/navigation map) is now generated prior to missile launch and ground launcher is now oriented to the first en-route waypoint. This prevents the cruise missile from making wild turns after boosting, allowing their launch signature to be better concealed within your spawn area. - M-ATV is now vehicle-based JTAC and moved to TA menu:
HUMVEE and MATV purchase options are swapped. HMMWV is now Light Utility Vehicle on the reinforcement menu; M-ATV is now airdropped jeep from TA. M-ATV now functions as vehicle-based JTAC – its offensive ability now provides JTAC laser designator. - New model for Spike NLOS Missile Launcher:
Replacing placeholder model with a real launcher model – much needed improvement.
5.5/Starscream is about 55% finished, and expected to be released around summer time.
Recent Developments:
Looking back through past 10 years, 2013-2014 was the most pivotal period for MW Mod – that is the time when FLINT reached version 4.0. FLINT 4 introduced significant backend features that were necessary to mature the mod to where it is today: features such as velocity-verlet integrator, linear interpolation (lerp) and introduction of execution environment for FLINT modules were all crucial to advancing the mod development forward.
Recently, FLINT and mod development have been going through a new round of improvements:
First of which is the improved interworking between FLINT scripts and server-side environment (known as WICG and EXGame), that allows us to create map-specific scripting and implement scripted missions or AI logics. In 5.5, we’re introducing very basic rudimentary scripted conditions (static unit emplacements in preset locations), but the future (MW Mod 6.0?!?) holds many promises – including an AI player interpreter that allows us to add more dynamic instructions (such as movement, Machine-Learning Reaction (mx.RE) system, etc) to gradually enhance the vanilla game’s bot AI, and allow room for scripted missions.
Second major development as of lately, is what is happening with air & missile defense (IAMD) component. Since the past year, we began migrating away from the legacy Patriot and IADS script code, and started moving to a single unified command & control (C2) system simulation, inspired after the US Army’s IAMD Battle Command System (IBCS) development in the real world, where air defense units could simply “plug in” to the network on demand (plug-and-fight capability).
In implementing C2 functions for the new IBCS system, what used to be a simple set of shooter scripts for AA has now turned into a Virtual Machine (VM) runtime environment running in Python, simulating a machine. The new IBCS Python modules now provide the following basic functions:
- Virtual Machine (VM) Runtime Environment with scheduler and dispatcher (known as Adjunct Processor (AP) Runtime System)
- Baseline support for execution stack and instruction pointers / program counters
- VM Interpreter written in Python with stack machine operations and predefined instruction set. Interpreter listens for unit state inputs and wic.Player pressed keys and compiles them into instruction stack, which is then executed by the bytecode dispatcher (under development). In the future, command & control functions (for engagement if-then situations) will move to predefined instruction set executed by the VM Interpreter, with players having the ability to influence the command & control behavior by pressing supported user input keys.
A recent fun example of the VM runtime environment is the new Counter-Battery Radar. When a counterfire radar is joined into the IBCS, a new “process” (called ‘jfired’) is started and dispatched accordingly by the VM scheduler.
Note that the VM scheduler lives inside the C2/EOC node (e.g. Fire Control Radar or Patriot site). If the current master EOC node is killed, VM scheduler & dispatcher functions are passed onto the next surviving EOC node. If all C2/EOC nodes are killed, VM runtime environment shuts down completely, and all IBCS units and processes cease functioning.
Future Roadmap and Challenges:
As we look toward MW Mod 6.0 and beyond, the above recent developments will allow the following:
- Gradual improvements and enhancements to AI system in game. By directly interacting with wicg environment, we can create more scripted conditions and dynamic Reaction systems based on predefined map parameters, helping to make AI player units more useful.
- The notion of adding naval units to select maps (where gameplay is feasible), is more and more inching closer to becoming reality. Improvements to Scripted AI allows non-human player owned ships to be added into the game, that are direct controlled by scripted AI with pre-defined pathfinding routes.
The new VM Runtime Environment for IBCS allows much easier integration and interworking of Naval combat system elements (such as Aegis, NIFC-CA), by using a common instruction set for unit C2 functions. THAAD is now also looking easier to add with the new VM environment. - At some point, we need to rewrite the aircraft (JTDS) movement and orientation scripts that were made back in 2011 (to make aircraft behave more realistically). Too lazy and lack of motivation is an issue on this topic however.
The challenge to all of this is time and motivation. Back in 2009-2011, MW Mod development was churning out new changes and units on almost biweekly basis at peak, monthly basis on average. Nowadays, getting anything new implemented in MW Mod often turns into over-engineered development hell. In some ways, MW Mod and FLINT are a victim of its own success over the past 10 years – with much heavier dependence on programming side of things, getting a unit added nowadays requires weeks for coding, testing and integration, thereby making things way more over-complicated than ever before. But it does look nice for sure!
We’ll see how the mod development continues in the future (6.0 and onward). But it seems rudimentary introduction of ships to a very few select maps is increasingly becoming likely.. We shall see.
A number of curious players have asked for more technical information regarding the air & missile defense system in game, such as information about what the individual messages mean on the chat display and how the system works under the hood. I've been meaning to do this for a while, but haven't found the time until recently.
About World in Conflict - Army Integrated Air & Missile Defense System (AIAMD)
The World in Conflict AIAMD is a multitasking weapons AI system that joins every Heavy SAM component units (known as 'nodes'), including sensors & command posts (radars, etc) and missile launchers into a single integrated domain, maximizing firepower against saturation air and missile attacks. Instead of one player individually engaging a given threat set, AIAMD networks your entire team's support elements into a netted architecture to engage multiple incoming threats.
The World in Conflict AIAMD is the most realistic simulation of air defense systems in the entire real-time strategy genre, with fidelity rivaling those of combat simulation titles such as Digital Combat Simulator and Falcon BMS.
Originally developed to counter cruise missile spams in multiplayer, the WiC AIAMD traces its lineage back to the Heavy SAM shooter scripts in 2010. Owing to this, the whole thing is largely a giant blob of linear evaluations and over 7,000 lines of monolithic code. Since World in Conflict MW Mod 4.7, we've slowly started to separate the monstrous blob of code into architecturally separated functions, with the goal of making the entire system more modular -- this will allow new battle elements and missile units to be added much easier in the future.
A fan-made video tutorial of the AIAMD in action is below:
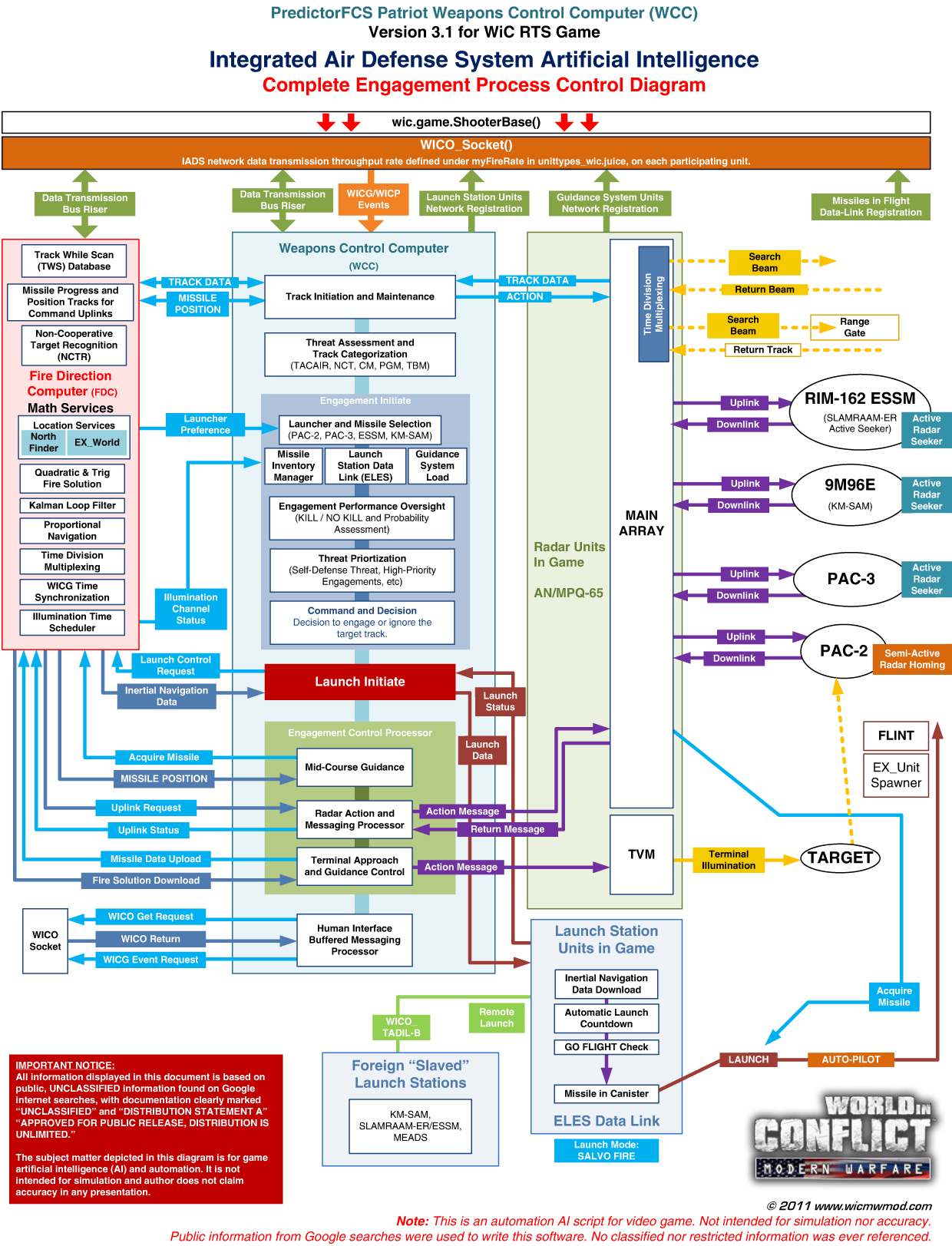
The AIAMD consists of the following major code functions: Adjunct Processor (AP), Radar Data Processor (RDP), Engagement Control Processor (ECP) and Launch Sequencer (LSEQ).
Adjunct Processor (abbreviated as AP; formerly called ADJP)
The Adjunct Processor is the primary scheduler that performs execution and governs every system unit elements in game (nodes). The AP performs administrative tasks, such as registering and admitting new units onto the network (called IFCnet) upon spawn, monitoring and requesting status from every node and providing interrupts and exceptions handling.
Human players can send system-wide abort signal to the AP by selecting battery units and Fire Control Radar and placing them into Hold-Fire (select units and press G key) for 2 seconds. Holding-fire for 2 seconds signals to the AP to initiate WPNS HOLD state. When entering weapons-hold, AP will issue abort signal (SIGABRT) to all running processes -- any missiles (birds) already fired and in the air will be given Command Destruct signal, detonating them in mid-air. Existing radar tracks will be gracefully maintained in memory for up to 10 seconds until at least one radar unit is returned out of hold-fire, or timed out and removed by watchdog.
Holding fire for more than 10 seconds will signal to AP to issue system-wide reload (SIGTERM) -- all tracks in memory will be erased and reset, every node in game will be re-registered as if a new match was started. Engagement performance data (percentage killed, # of missiles expanded, etc) and missile ammunition states however will be kept through system reloads until the match ends.
When encountering rare errors, AP gracefully handles exceptions to prevent Heavy SAM units from ceasing to work for the remainder of the match. If there is a math error while guiding a missile onto its target (quite rare, but happens sometimes; e.g. division by zero error), ADJP raises MDL.H-Loop exception and sends Command Destruct to the outgoing missile and resets engagement state for the target track, allowing it to be re-engaged. Code-defined Assert failures caused by an individual outgoing missile will terminate the errored missile (command destruct message) and unhandled exceptions (including wic.game unit exceptions) will trigger PROG HALT and issue system-wide reload of all units.
Radar Data Processor (RDP)
The RDP runs Track Initiation and Maintenance and Engagement Initiate processes. For track initiation, RDP function performs Volume Scan loop at every frame. Each individual radar unit (MPQ-65) derives its scan volume by drawing an area of scaled 22,500km^2 and cropping it to radar's boresight sectors (110 degrees). Target detection occurs when game is providing LOS vision (fog of war) against the target, and when the target falls inside radar's boresight sectors. When a new target is being added, an evaluation is performed to determine target type and crudely check for detection requirements. Although not modelled today, in the future, a library of radar cross sections (RCS) and radar range equations will be added to model detection of targets with varying RCS and electronic countermeasures (ECM). For simplicity sake and performance reasons, friendly air and missile units are completely ignored by the system and not even considered.
When a detected target is successfully recognized, a track file is initiated and the target is assigned with a track number. Any further updates to this target's behavior and position changes will be recorded onto its track data. Each radar in game can maintain up to 100 tracks.
The RDP uses the Track While Scan (TWS) principle. While the radar is searching for new targets within its assigned scan volume, Engagement Initiate process known as TWS_Loop() is also run on every track to continuously track target position and velocity changes. Target tracking requires the established track to be within +/-90 degrees boresight from MPQ-65 battery radars -- if the target is outside of boresight from all available battery radars, the track is dropped. This makes Patriot SAM in game a "sectored system" -- targets falling outside of 110 degrees radar tracking fan cannot be tracked successfully.
There are two ways to work around the sector limitations of Patriot in game: (1) you can select each battery squad and use force-fire (hold F key then left click on desired azimuth) to lock the radar into the desired azimuth. By having more than one Heavy SAM squad, you can assign each squad with different boresight azimuths, thereby allowing you to cover 220+ degrees; and (2) alternatively, you can spawn a NATO Fire Control Radar unit -- the NATO MFCR (MEADS) is a command post unit with 360-degrees rotating tracking radar, allowing all tracks to be maintained regardless of boresight limitations.
For tracking of targets via TWS (such as aircraft, etc), the track maintenance process uses Range Gating to update each track. At each radar return hit, the RDP applies target's velocity and predicts its position at the next tracking run. The target's predicted position is "blocked out" (gated) by range and azimuth from the radar. During the subsequent tracking run, the RDP only scans this predicted area (gated range and azimuth) to validate whether the target has walked into it. If so, tracking is marked with a successful HIT and a new range gate is calculated for next scan. If the target continues to successfully fall inside predicted range gates repeatedly, the track is passed onto Engagement Initiate to be considered for engagement. If the target is ejecting countermeasures and flying very unpredictably in a short period of time (within 2-3 seconds), target may not be detected inside the predicted range gate -- in this instance, a track MISS counter is updated and the target is continuously tracked until it falls back into range gate. If the target continuously evades radar's prediction in this manner, track is re-classified to Non-Cooperating Target (NCT) and ignored for engagement until it can be tracked successfully again.
A simple way to describe Range Gating routine would be Air-to-Air Strike tactical aid (A2A TA) in the vanilla unmodded World in Conflict. Try targeting a moving air player in middle of his flight by predicting his position 10 seconds ahead and laying down the A2A TA. If the air player walks into the circle successfully in 10 seconds, that's considered a HIT.
Engagement Control Processor (ECP)
ECP runs when system commences automatic engagement against one or more target tracks. When an automatic engagement begins, the RDP downlinks messages to the Launch Sequencer (LSEQ) to request missile launch against the track being engaged. Once a launch station fires its missile, the LSEQ reports back to ADJP with launch-success message and the track ID of the outbound missile (bird) that has been launched on track. ECP then takes over to govern the outgoing bird's flight from beginning to the end.
Once a bird is in the air, the ECP establishes a socket for the outbound missile to "ping" back to the radar on its position -- this is called Missile Down Link (MDL). The outbound bird is a FLINT missile unit which upon spawn, joins IFCnet and initializes inertial navigation system. The missile will begin flying toward the inertial navigation point that was fed to it by the launch station -- 1.5 seconds after a successful launch and when the missile has cleared some distance away from the launcher, the bird will report in via datalink to the ECP with its position and Time to Go (TGO) estimation. The ECP then commences Mid-Course Guidance against the engaged target track. If the bird is unable to establish an MDL connection to the ECP (because radars got killed by enemy HARMs etc), the missile will time out and self-destruct due to loss of the command data-link. In the event of a system abort (SIGABRT), ADJP will command ECP to uplink Command Destruct message over the MDL to all outbound birds receiving mid-course guidance updates. Birds receiving Command Destruct signal over MDL will immediately self-destruct in the air.
After establishment of the MDL data-link with outbound birds, the engagement process consists of Mid-Course Guidance and Terminal Guidance. Each outbound bird is equipped with an auto-pilot using inertial navigation system. The inertial nav point provides the bird with range-to-go and azimuth information toward the Predicted Intercept Point (PIP), better known as "the kill box" or "basket". The PIP is calculated and updated by the RDP as it continues to track the target -- as PIP changes over time, the ECP uplinks new updated PIP position data to the bird, causing the bird's inertial navigation system to adjust its course to the new updated target position. The missile sends return message back over MDL to confirm that it received an updated PIP, and also sends its own Time to Go (TGO) estimation toward the PIP basket. Once the missile arrives near the PIP, terminal guidance commences.
The terminal guidance method differs depending on the type of bird used, however the goal of the terminal guidance is to resolve ambiguity on target's exact position and move in for the final kill. Because TWS process used by radars is not accurate enough, terminal guidance requires a more powerful method of tracking to resolve the exact range and vector states of the target.
- For PAC-2/GEM-T missiles, upon arriving near the PIP basket, the ECP commands the bird to open up its seeker via MDL and commences Single Target Track (STT) by illuminating the target with ground radar at very high pulse repetition frequency (high PRF). The bird then begins "streaming" boresight errors (how much it is off from the target LOS) back to the ECP via downlink messages. The ECP then compares the missile's reported boresight errors and the target position to calculate an intercept solution using Proportional Navigation, and uplinks the new acceleration command back to the missile. The missile then steers to meet the new acceleration command and the whole process repeats in a loop until intercept. This loop is called Track-via-Missile (TVM) guidance -- it is a form of Semi-Active Radar Homing (SARH) and basic principle is similar to semi-active laser homing missiles in game (e.g. Hellfire and LGBU).
The ECP can "redirect" an outbound PAC-2/GEM-T bird near the basket onto another target by simply redirecting the illumination beam onto the next target. This allows the Patriot radars to "walk" outbound birds onto multiple targets in series. Because the SARH / TVM process only lasts between 2-3 seconds, this allows "time-shared illumination", allowing a single illuminator to support engagement of multiple targets by walking its beam from one target to another, separated by 2-3 second intervals. - For PAC-3 missiles, upon arriving near the PIP basket, the missile opens up its active radar seeker and downlinks boresight errors (how far it's off the target) to ECP via MDL. The ECP replies back with exact boresight fix on the target track relative from the missile's own seeker, allowing each PAC-3 missile to individually identify the assigned target for it to make the kill (this provides target de-confliction when multiple PAC-3 missiles are in the PIP basket trying to find a target). Once the bird receives boresight confirmation from ECP, it drops the ground data-link by disconnecting from MDL and commences active radar terminal homing (gone "pitbull" in air force parlance).
Unlike SARH/TVM method above, the PAC-3 missile calculates its own intercept position in game by using its own radar seeker. Because the missile is entirely on its own at this stage, it can no longer be controlled by ground radars once it has gone terminal -- if a Command Destruct message is sent to a PAC-3 missile after it had gone terminal, it will not self-destruct, and will still go after its target uncommanded, or time out and self-destruct if no target is available. Moreover, if assigned target is not visible within missile's FOV, missile will try to search for any other targets visible within the seeker FOV. If a new target is seen, it will lock onto it and try to kill it.
During game development, there had been cases where airborne PAC-3 missile had uncommanded engagements of unexpected enemy targets (such as an R-77 air-to-air missile, or a BM-30 artillery rocket), that happened to be flying in the same PIP killbox as where PAC-3 was flying.
Launch Sequencer (LSEQ)
The Launch Sequencer (LSEQ) module manages every missile launcher (known as Launch Stations or LS) in the AIAMD network in game. The LSEQ also provides scheduling of launch orders as received from RDP.
The LSEQ polls every LS in game for ammunition states and missile type available in magazine. The ammunition state data is fed back to the ADJP which is then used by RDP to create an engagement plan. During Engagement Initiate process, the RDP uses ammunition state information to select which type of interceptor to use against the target -- the RDP will prefer to use PAC-3 missiles against ballistic missiles, while reserving PAC-2/GEM-T missiles for aircraft and cruise missiles, etc. The RDP also decides on engagement doctrine (SHOOT-LOOK-SHOOT, RIPPLE, SALVO, etc) and how many interceptors to fire onto the targeted track, based on the ammunition state reported by LSEQ.
When RDP commences engagement process and requests missile launches onto targeted tracks, LSEQ begins receiving launch orders. LSEQ then begins scheduling launch orders based on track priority as scored by the RDP. Launch sequencing is always scheduled in the following order of priority: (1) theater ballistic missiles; (2) rocket artillery and mortar; (3) cruise missiles and precision-guided munitions; and finally (3) aircraft. Launch orders are categorized and prioritized by their track classification -- in each track type, launch orders are further re-prioritized based on urgency. Tracks that need to be engaged soonest (because they are closest to breaching defended asset, or are Self Defense Threats targeting a Patriot battery) are prioritized to the front of the launch sequence queue.
When LSEQ runs, it polls and waits on every launch station (LS) that have the appropriate ammunition available to report in. LSEQ will use position of each LS and the kinematics (Time to Go) data provided by RDP on the target track to select the launcher with best possible kinematics and probability of success. The launch order is then assigned to the selected LS with the requested ripple or salvo size.
If the selected LS was unable to complete its fire mission (could not fire all missiles requested in the salvo size, because launcher got killed or ran out of ammo prematurely), LSEQ will then re-compute the next best available launcher and re-assign the fire mission to another LS.
The most important purpose of the LSEQ is to always provide high firepower to meet any attack size as requested by the mission parameter, so long as it has ammunition available to fire.
During a saturation missile attack raid, LSEQ launch request queue will be filled with more requests than there are number of launch stations available with ammo, or with the number of fire control resources (illuminators) available. If the system is running low on ammo to meet the mission parameters, instead of focusing on ripple fire on each target (firing 2 missiles per target, separated by 2-3.5 second apart), the LSEQ will prioritize firing 1 interceptor against as many number of target tracks it has in the queue.
The LSEQ always attempts to service the largest number of targets in a queue using the given set of ammunition resources available. Ripple and salvo firing of more than 1 missile per target will only occur when there is more ammunition available in excess of the launch request size.
If the salvo size exceeds the number of fire control resources available, LSEQ staggers missile launches to schedule the time-shared illumination. Because each LS has a minimum enforced rate of fire (the time it has to wait between each individual launches, to allow backblast to clear the launcher and to prevent overheating of mechanical structures), LSEQ uses Time Division Multiplexing (TDM) to sequence launch requests in a series of time slots.
Imagine having two LS, each with enforced wait time of 3 seconds between launches -- instead of firing both launchers at once and waiting 3 seconds on both of them, LSEQ will assign launches to both launchers, with each launch separated by a time slot of 1.5 seconds. This allows a missile to always be continuously launching out of both launchers every 1.5 seconds apart, while still meeting the 3 seconds wait time for each individual launcher. While first LS is dwelling and waiting for its 3-seconds hold time between launch, the second launcher is firing 1.5 sec later -- after another 1.5 sec time slot has elapsed, first launcher can fire again, and the process repeats.
By staggering missile launches in time slots using TDM, LSEQ enhances the ability for the ground radar to "walk" its illumination beam among different targets during terminal stage.
Understanding Status Messages in Chat
The ADJP will report back to the player with status of the AIAMD system via chat messages in the game. Although most messages here are self-explanatory, several players have asked for detailed explanation of each term and the telemetry data that is given. The Status Message typically looks like this:
SystemName MSL INVENTORY: GEM-T 33 PAC3/CRI: 32 TAMIR: 40 LS OPER: 16 LS STBY: 1 RELOAD: 54.1 sec
4 AIR, 1 NCT, 7 UNK [TLL: 7.1s], 1 CM/PGM[SDT], 0 RAM, 1 TBM [TOF: 13.1s TLL: 9.7s]
TVM: [11.1% 1/9] ADJP: [SchedulerState] 14 tracks: [3 TWS, 1 TVM, MA 06, TGO 07]The first line shows the overall system status, engagement performance and ammunition available. The first line will cycle between various states to show ammunition status on every possible interceptor available, as well as engagement performance (ratio of tracks killed vs. tracks engaged) and how many rounds have been expanded. "LS OPER" means launch stations in Operation State -- this is the number of LS that have at least 1 interceptor available in its ammo to fire. "LS STBY" means launch stations in Stand By state -- this indicates the number of LS that are out of ammo and reloading its magazine. "RELOAD" indicates the launcher with the shortest amount of reload time left to replenish its ammo.
"SystemName" in the first line will either state "Patriot WCC" or "AIAMD EOC." If it displays "Patriot WCC", it means the system is relying on classic sectored battery radars (MPQ-65) on each Patriot fire unit/Heavy SAM squad -- there is no 360 degree coverage and the coverage is defined by where each battery radar is facing (you can set the desired azimuth by using force-fire on the Heavy SAM squad).
If the SystemName displays "AIAMD EOC" it means the Patriot system is operating in Integrated Battle Command System (IBCS) mode and 360 degrees tracking coverage is provided -- every launch station and radars are enrolled into the fire control network (IFCnet) as nodes to enable "sensors and shooters on the net" operation, disengaging the system from the old sectored model.
To operate in IBCS mode, you will need to spawn a NATO Fire Control Radar (MEADS) unit from the support panel -- enable the MEADS FCR's offensive special ability and force-fire it anywhere to commence 360-degree operation.
The second line shows the radar tracks and telemetry of the most pressing track in each category. Radar tracks are classified by the following types:
AIR: Aircraft deemed hostile
NCT: Non-cooperating target (prevented from engagement but still tracking)
UNK: Aircraft in unknown intention (system is identifying whether the target is hostile or can be ignored)
CM/PGM: Cruise Missile/Precision Guided Munition
RAM: Rocket-Artillery-Mortar
TBM: Theater Ballistic MissileOn each track category, telemetry data is shown on the most highest priority track within the given category inside brackets. TLL means Time to Last Launch -- this is the amount of time (in seconds) available for us to engage the target before the target breaches a Defended Asset or the final line of defense. TLL is calculated by predicting the target's vector and calculating whether our missile will intercept the target in time before it breaches the "keep out" line for the defended asset. When the TLL goes negative, it means the target will have breached the defended asset by the time our missile arrives to kill it.
TOF means Time of Flight and TOF telemetry is displayed for both RAM and TBM targets. TOF is the estimated time until the ballistic target breaches the minimum "keep out" altitude where it could no longer be engaged. TLL is also calculated as described above, showing the amount of time we have to launch on the ballistic missile before we could no longer engage it.
When a target track is heading directly toward an AIAMD battery asset or otherwise threatening it (e.g. launching a cruise missile at you), the telemetry data will show red "SDT" flag inside the brackets. SDT means Self Defense Threat and the system will automatically prioritize SDT to be engaged first, ahead of other targets.
The third line displays overall system status. TVM means Track-via-Missile and inside its brackets, it indicates the number of tracks being illuminated for semi-active radar homing, over the number of illuminators available. Each MPQ-65 Patriot battery radar has 9 illumination channels available for TVM terminal guidance. In the above example, our TVM illuminators are 11.1% utilized, as we are illuminating 1 target currently, out of radar's 9 channels. The more radars you have, the more illumination channels you have.
Note that TVM is only applicable for the older PAC-2/GEM-T missiles, which require SARH guidance during terminal stage. For PAC-3 missiles, TVM is irrelevant -- those missiles have onboard active radar seekers and do not require SARH illumination from ground radars, so TVM capacity means nothing for PAC-3.
The next field displays the Adjunct Processor (ADJP) scheduler state -- it displays the most significantly running process at the given time. The ADJP SchedulerState is defined as follows:
MBI BOOT: Minimum boot image booting -- this is displayed when system is booting up in the background, creating data arrays and registering all nodes into the fire control network. You will typically see this message when system is starting for the first time, or has restarted due to period of inactivity or due to system error causing a restart.
RDP RUN: Radar Data Processor running -- indicates that RDP is volume scanning, tracking targets and making engagement decisions.
WPNS FREE: Weapons Free (rarely seen) -- briefly and rarely seen; this message is displayed typically when the RDP has given "Weapons Free" state to let others know that engagement is about to start, but the target is not yet within the missile's kinematics envelope to be fired upon yet. Launch stations have been issued with launch authority and will fire as soon as the target walks into missile's kinematics range. Because targets are typically engaged well inside missile's kinematics range, you will rarely see this message; however, you may briefly see WPNS FREE message when engaging targets such as medium-range ballistic missiles (MRBMs), where launch authority is given before the ballistic missile has breached the PAC-3 commit altitude.
ENG HOOK: System has selected a specific track ("hooked track") to be engaged and Engagement Control Processor (ECP) is running on the target. Rarely displayed as track selection often happens very quickly.
ENG AUTO: Engagement Control Processor (ECP) is running and executing on full automatic mode against multiple targets. Indicator message blinks every second.
LSEQ WAIT: Waiting on Launch Sequencer (LSEQ) to schedule missile launches. Often happens when there are more targets than there are launch stations (LS) with ammunition to fire. If you are seeing this message for a long time, that means your defenses are saturated -- you will need more launchers to relieve saturation. You can purchase more PAC-3 launchers via airdrop from the Tactical Aid menu. If you are seeing this message only briefly, that's usually fine and no action is needed -- LSEQ will eventually adjust fire doctrine as long as there is still ammo available.
LSEQ BUSY: LSEQ could not accomplish priority fire mission because launchers are saturated. If you are seeing this message often, you've really run out of missiles -- buy more airdropped PAC-3 launchers from TA.
The last part of 3rd line shows the total # of tracks on the radar -- "# in TWS" means number of tracks currently being tracked for engagement process, "# in TVM" means number of tracks currently being illuminated by ground radars for PAC-2/GEM-T terminal guidance. "MA" means Missiles Away -- total number of birds that are currently flying in the air.
Finally "TGO" means Time to Go -- estimated time until intercept. Outbound missiles constantly calculate TGO using their inertial navigation and downlinks it back to the ECP. The ECP will display the most minimum, smallest TGO of all of the birds that are currently flying. Note that TGO is only updated during mid-course update -- it will stop updating once the missile has gone terminal and MDL data-link had been terminated.
Types of Missiles
The World in Conflict AIAMD utilizes the following missile types in game to defeat a wide array of airborne threats:
GEM-T (PAC-2): The classic Patriot missile -- uses semi-active radar homing (SARH) using TVM guidance:
Each Patriot Heavy SAM unit comes with 6 launchers each having 4x GEMT-2/PAC-2 missiles. GEM-T can engage both air breathing targets and ballistic missiles. Its defended footprint against ballistic missiles is limited and engagements can occur up to 15km altitude. GEM-T uses blast fragmentation warhead with proximity fuze to defeat the target -- because of this, the probability of kill against high speed ballistic missiles (such as MRBMs) is lower. Against short range battlefield ballistic missiles (such as Iranian Zelzal II in game) and air breathing targets such as aircraft and cruise missiles, GEM-T is highly effective and available at low, economical cost.
Once GEM-T commences terminal homing using TVM, it is extremely difficult to jam it with countermeasures -- because both the ground radar and the missile seeker are in the loop and tracking you simultaneously, enabling countermeasures to blind the ground radar does nothing, as missile seeker is still reporting what its seeker is seeing back to the radar. The key to defeat GEM-T from helicopter perspective is notching by flying very low, or drop countermeasures early before the missile has gone terminal, and fly out of the area.
PAC3/CRI: PAC-3 Cost Reduction Initiative missile (also known as ERINT):
This is the classic PAC-3 missile initially introduced in 2003, and upgraded in 2008-2011 periods. The PAC3/CRI uses kinetic "hit to kill" impact to destroy its target and has an active radar seeker -- because of the active radar seeker, PAC-3 missile does not need to be supported with SARH illuminators during terminal stage. PAC-3 missile allows high firepower against saturation attacks -- up to 16x PAC-3 missiles can be packed on a standard M902 launch station, quadrupling the amount of missiles from PAC-2/GEM-T. Due to the use of active radar seeker and eliminating the SARH requirement for terminal guidance, PAC-3's only firepower limitation in theory is the magazine depth (i.e. how many PAC-3 missiles you have vs. # of targets incoming).
Each Patriot Heavy SAM squad in game has two LS loaded with PAC3/CRI missiles. For game balancing reasons, each Patriot Heavy SAM squad in game is only loaded with half packs of PAC3 (2 canisters as opposed to 4), so each PAC3 LS in squad only has 8 missiles, as opposed to 16. However, if you spend 25 TA to purchase airdropped PAC-3 launcher from tactical aid, you'll receive a fully equipped launcher with 4 canisters, giving you 16 missiles each.
PAC3/MSE: PAC-3 Missile Segment Enhancement (MSE):
This is the latest upgrade to the Patriot system and started entering into limited service in 2016. Mass production of the PAC-3 MSE was started in 2017. The PAC-3 MSE effectively doubles the altitude and range of the classic PAC3/CRI missile. Utilizing the dual-pulse solid rocket motor, the PAC-3 MSE fires its second pulse during terminal stage as it maneuvers aggressively to make the kill. This gives MSE a much more increased maneuverability and energy to successfully intercept very high velocity ballistic missiles such as MRBMs (North Korean No Dong, etc) and maneuvering ballistic missiles (Iskander) in game.
To give you a perspective, against Iskander maneuvering SRBM in game, PAC3/CRI's effective range against Iskander is halved -- it can cover only about quarter of the map from the launch station; at any further distance, Iskander will aerodynamically defeat the interceptor through its evasive maneuvers. PAC-3/MSE however will cover nearly the entire game map against maneuvering Iskander and still has enough energy to match the evasive maneuvers and intercept.
The PAC3/CRI reaches up to 20km altitude in game against ballistic missiles, while PAC-2/GEM-T reaches up to 15km altitude. PAC-3/MSE can reach up to 32km altitude in game. The PAC-3 MSE missile can only be purchased via Tactical Aid using airdropped launcher -- there are only 12x PAC-3 MSE missiles per launcher, as opposed to 16x on PAC3/CRI.
PAC-3/MSE is useful to counter saturation missile raids from high velocity No Dong MRBM attacks coming from REDFOR team. PAC-3/CRI is useful to counter saturation missile raids from short range ballistic missiles such as Tochka, Iskander, etc. Additionally, if you want to cover the entire map distance with the minimum number of launch stations, PAC-3 MSE will cover the whole map (whereas PAC3/CRI will cover 2/3rd to 1/4th of the map depending on target's speed)
It is a good idea to mix both PAC3/CRI and PAC3/MSE launchers simultaneously in game -- this will provide a balanced mix of increasing defended footprint against ballistic missiles of all types, and increase firepower against saturation attacks (you'd see MSE's flying out to engage MRBMs up to 30km high, then follow on with PAC3/CRIs to catch any leakers or provide further layer of defense.
TAMIR: This is the interceptor for Iron Dome launcher in game:
Tamirs are only used by the AIAMD system to defeat Rocket-Artillery-Mortar (RAM) targets. The system will only expand Tamirs against incoming rocket artillery. If you are out of Iron Dome missiles, you can provide a second tier of defense using airdropped Phalanx C-RAM -- though Phalanx guns are easily defeated by saturation barrage. Coupling Iron Dome coverage with C-RAM will provide a very robust defense against rocket artillery. Note that both the Iron Dome and Phalanx C-RAM are completely useless (will not even fire) against ballistic missiles. Only the big boy missiles (e.g. PAC-2, PAC-3/CRI, PAC-3/MSE) can engage ballistic missiles.
THAAD: Terminal High Altitude Area Defense -- not yet implemented in game:
(will be introduced in future MW Mod 5.x release) When implemented, THAAD will only engage medium range ballistic missiles (MRBMs, so only No Dong missile in the game), but at a whopping 150km altitude in the edge of the space. With the engagement zone covering from 40km to 150km altitude, THAAD and PAC-3 MSE working together can provide a true "SHOOT LOOK SHOOT" capability for ballistic missile defense, where only 1 interceptor can be fired against the target, and still have time to fire a second interceptor if the first intercept fails. To introduce THAAD, gameplay changes to MRBMs will also need to be made for balancing reasons.
IFPC: Indirect Fire Protection Capability -- not yet implemented in game:
(will be introduced in future MW Mod 5.x release) This is a mobile frontline FMTV truck with 15-cell multi-mission missile launcher (MMU) that players can deploy and bring with them anywhere on the map to provide frontline air defense coverage. The MMU cells will be loaded with a mixture of Evolved Sea Sparrow Missile w/ active radar seeker (ESSM Block II/SLAMRAAM-ER) for defense against aircraft and cruise missiles, Tamir/Iron Dome missiles for counter-rocket artillery, and Longbow Hellfire missiles for anti-tank/ground targeting support via offensive special ability. The IFPC truck will have to "join" the AIAMD network by enabling Defensive Ability (just like on Patriot SAM launchers) -- once joined into the network, Patriot and MEADS radars in the AIAMD network will remote-control the IFPC trucks for air defense operations. The IFPC should provide a refreshing upgrade from Stinger SHORAD SAMs for armor & infantry players.
The Future
With the recent revival of World in Conflict (www.massgate.org) community, there is now once again a case for continued and renewed development for MW Mod. While infantry role has now become the best role to play in WiC MW Mod (largely due to the infantry's ability to call on fire support channels and being able to dance all around the map with high mobility), air and missile defense (IAMD) continues to remain one of the most critical show pieces for the mod since its inception. Therefore, air defense will continue to evolve in MW Mod along with frontline force units.
Although air defense system was originally made to automate engagement against saturation missile attacks, the future of AIAMD in MW Mod 5.x is to evolve the air defense into a fully netted architecture that can be influenced by frontline infantry and armor units. Instead of air & missile defense solely being support player's role in the game, the future of air & missile defense in MW Mod will be a "plug and fight" architecture where the support player provides the baseline infrastructure with heavy sensors and massive firepower (missile defense radars, Heavy SAM, etc), and infantry and armor will "plug in" their own systems to specify where to defend, allowing the entire AIAMD network to dynamically adjust coverage on the move for infantry and armor.
In this tutorial, I will provide a brief overview of proportional navigation family of guidance laws, but more importantly, we will go over some sample code so you get straight to trying it out in your own game. This tutorial (and accompanying demonstration video) is written using World in Conflict MW Mod. Sample codes are written in Python for MW Mod's FLINT Missile System.
History of Proportional Navigation (PN)
PN is the foundation of modern homing guidance in virtually every guided missiles in use today. The theory of PN was developed by the US Navy during World War II as desperate measures were needed to protect their ships from Japanese kamikaze attacks, and gun-based defense systems (even automated fire director controlled guns) simply did not have the range to take out the target at a safe distance, and easily became overwhelmed by saturation. Automatic homing missiles were urgently needed to defend ships at sea.
Although theory of PN was apparently known by the Germans during WW II, no applications were reported and the war shortly ended thereafter. The US Navy's experimental Lark missile was the first to implement PN, soon followed by Sparrow and the venerable AIM-9 Sidewinder after the war.
PN is cheap to implement and had demonstrated to provide effective homing guidance-- It is because PN does not require geometry information such as range to target and target speed (though it can also benefit from it), making it ideal to implement on simpler "range-denied" missiles, such as passively heat-seeking IR missiles and semi-active laser homing variants. Not only that, the theory of using Line of Sight (LOS) information to develop collision course is such a powerful concept, that virtually every advanced guidance laws used today share their ancestry lineage back to PN. If you ever see people attempting to code so-called "advanced target homing" missiles in games using quadratic equations and trigonometry, you can clearly see that they're reinventing the wheels and got some learning to do :-) PN totally laughs at, and beats out every other forms of homing guidance used by games, which integrate states by solving for what is essentially a high school geometry.
Understanding Theory of PN
PN works on the principle of "Constant Bearing Decreasing Range" (CBDR), where when two objects are heading in the same direction with no change in Line of Sight (bearing) angle, objects *will* collide. Line of Sight (LOS) is an imaginary sight-line between you and the target; when target is moving from left to right in your field of view, it is said that the LOS angle is changing from left to right. If however, you were to also run from left to right and accelerate appropriately to keep the target centered in your field of view, it is then said the rate at which LOS angle is changing (LOS rotation rate) is zero ("null"). Continuing to run with LOS rate maintained at zero will result in intercept and "lead to pursuit" collision with the object you're chasing.
Mathematically, PN is stated as follows:
Commanded Acceleration = N * Vc * LOS_Rate
N = Unitless navigation gain (constant) -- between 3 to 5
Vc = Closing Velocity (or "range closing rate")
LOS_Rate = LOS Rotation Rate
To describe this along a two-dimensional missile-target engagement geometry:
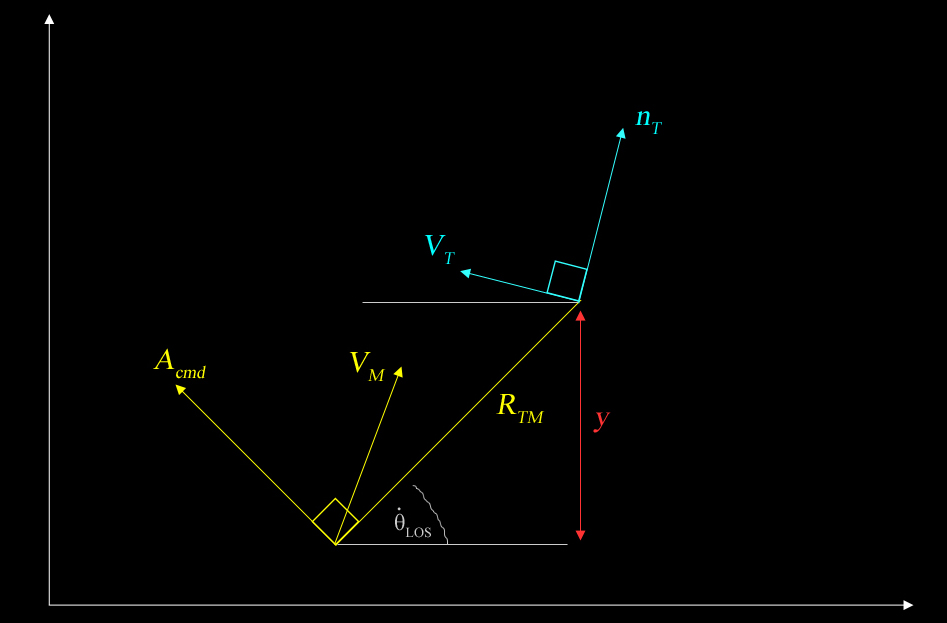
When working with PN, it is important to understand that missile's acceleration is commanded (Acmd) normal to (aka perpendicular to) the LOS, and proportional to the LOS rotation rate. LOS as stated earlier, is the sight-line between missile and the target, which would be "Rtm" line in the above diagram. LOS rotation rate is the angular rate at which the LOS line changes -- denoted by the over-dot theta "LOS" grey angle in the diagram above.
Prerequisites
Before we get started, we first assume that you already have very basic knowledge in implementation of homing missiles in game. If you are this far, you probably know that in order for your game physics to work, you need some sort of integration scheme (i.e Euler, Verlet, Runge-Kutta 4, etc) that provides step-by-step numerical integration at every frame. FLINT missile system in WiC MW uses Velocity-Verlet, but essentially, what it all comes down to is simple: you step forward one step (or frame) at a time and solve for your states. If you need help with game physics and integrators, check out Gafferongames.com
Implementing PN in Game
Now, to implement PN, we need to fill in the blanks from the above equation "An = N * Vc * LOS_Rate." Let's discuss how to obtain the individual input variables to calculate our required lateral acceleration (latax).
1. Obtaining the LOS Rotation Rate (LOS_Rate)
As explained above; LOS Rotation Rate is the rate at which target is crossing your field of view, or more exactly, the rate at which sight-line angle is changing.
Obtaining LOS_Rate is easy, especially in game environment. In real life, the missile seeker sits on a gimbaled gyro -- the seeker rotates in the gyro to keep the target locked on; the rate at which it rotates is your LOS rate. In real life, engineers have to contend with seeker noise contamination, but in games, we're essentially working in a noise-free environment.
First, you need to obtain the directional vector between the missile and the target (remember "Rtm" in the above diagram?) -- this is your LOS:
RTM_new = math.Vector3( targetPosition ) - math.Vector3( missilePosition )You will measure and record LOS at every frame; you need to now get the difference between the new RTM (RTM_new) you just measured, and the LOS obtained from the previous frame (RTM_old) -- this is your change in LOS (LOS_Delta).
RTM_new.Normalize()
RTM_old.Normalize()
LOS_Delta = ( RTM_new - RTM_old )
LOS_Rate = LOS_Delta.VectorLength()2. Closing Velocity (Vc)
Closing Velocity (Vc) is the rate at which the missile and the target are closing onto one another. In other words, as the missile is traveling toward its target, it gets closer to the target, no? So, the rate at which our missile is closing the distance to its target is called the "range closing rate" or simply "closing velocity." This range rate is mathematically defined as follows:
Vc = -Rtm_overdot
-Rtm_overdot = Negative rate of change of the distance from the missile to the target.Now, this raises a curious question: How do you obtain 'range rate' on a passive heat-seeking missiles that have no radar to measure distance? Well, you guesstimate it (lol) -- that's what the early rudimentary version of Sidewinder in 1953 did. Doesn't work very well against accelerating or maneuvering targets, but it was effective enough for what was world's first PN heat-seeking missile. In modern versions like the AIM-9L, AIM-9X, Stinger etc, you have computation power available in the seeker to "process" the intensity of IR or the image it sees. As IR signature gets closer, it gets more intense -- the rate of intensity change is your range closing rate.
On radar guided missiles, including semi-active homers like the original Sparrow missile, you have better luck! On a radio-frequency based sensor, the seeker can observe Doppler frequency of the target return to calculate the rate at which the missile is closing onto its target. Doppler effect is quite measurable on wavelengths as you get closer or away from the target. Negative rate of change in Doppler frequency is the closing velocity.
Anyway, now let's back to our in-game code. Recall from earlier that we derived our LOS_Rate in vector space as the difference between the current frame's missile-target vector (RTM_new) and the previous frame's missile-target vector (RTM_old). The length of the vector for this difference is denoted as LOS_Rate above. Well, just so it happens, as our missile is closing onto the target, RTM_new is shorter than RTM_old! So LOS_Rate length itself is a rate of change in missile-target distance. Then, conversely speaking, the negative rate of this distance change is our range closing rate, aka the closing velocity:
Vc = -LOS_Rate
3. Navigation Gain (N)
Navigation gain (or navigation constant) is a designer-chosen unitless variable usually in the range of 3 to 5. Higher the N, the faster your missile will null out heading errors. Generally, it is recommended for N to stay between 3 to 5. FLINT missiles in WiC MW use N of 3; most missiles in real-life use 3 as well.
4. Augmented Proportional Navigation (APN)
When implementing PN, it is best practice to focus on target's acceleration normal to LOS'-- we're using a missile to hit a moving target after all. What does 'acceleration normal to LOS' mean exactly? Well, as the missile is homing onto the target, the target would most likely move laterally, or 'perpendicular to' along the LOS sight-line (crossing target would present the most movement normal to LOS).
The reality is that, often times the target is not moving at a constant velocity -- it changes directions, or it slows down or accelerates. You also have upward sensible acceleration of 1 G even for non-maneuvering targets if you're simulating gravity.
To account for these factors, you add a term to our PN formula by adding "(N * Nt ) / 2":
Commanded Acceleration = N * Vc * LOS_Rate + ( N * Nt ) / 2
Nt = Target acceleration (estimated) normal to LOS
Even for targets that do not maneuver, the target's one-g sensible acceleration is multiplied by N/2, producing a more efficient intercept.
Putting it all together - Sample Code
Below is a sample FLINT missile system code for FIM-92 Stinger heat-seeking missile, written in Python. It is the simplest missile in game to employ augmented PN, as it's a passive heat-seeking missile.
def GCFLINT_Lib_APN( msl_pos, tgt_pos, msl_pos_previous, tgt_pos_previous, latax, N = None, Nt = None ):
"""
Augmented Proportional Navigation (APN)
A_cmd = N * Vc * LOS_Rate + N * Nt / 2
msl_pos: Missile's new position this frame.
tgt_ps: Target's new position this frame.
msl_pos_previous: Mutable object for missile's position previous frame.
tgt_pos_previous: Mutable object for target's position previous frame.
Set these objects to "0" during first time initialization, as we haven't
yet started recording previous positions yet.
latax: Mutable object for returning guidance command.
N: (float, optional) Navigation gain (3.0 to 5.0)
Nt: (float, optional) Target acceleration amount normal to LOS
"""
import wic.common.math as math
from predictorFCS_flint_includes import *
from predictorFCS_EXFLINT import *
if N is None:
# navigation constant
N = 3.0
else isinstance(N, float) is not True:
raise TypeError("N must be float")
if Nt is None:
# one-g sensible acceleration
Nt = 9.8 * EXFLINT_TICKTOCK
else isinstance(Nt, float) is not True:
raise TypeError("Nt must be float")
if msl_pos_previous is not 0 and tgt_pos_previous is not 0:
# Get msl-target distances of previous frame and new frame (Rtm)
RTM_old = ( math.Vector3( tgt_pos_previous ) - msl_pos_previous )
RTM_new = ( math.Vector3( tgt_pos ) - msl_pos )
# normalize RTM vectors
RTM_new.NormalizeSafe()
RTM_old.NormalizeSafe()
if RTM_old.Length() is 0:
LOS_Delta = math.Vector3( 0, 0, 0 )
LOS_Rate = 0.0
else:
LOS_Delta = math.Vector3( RTM_new ) - RTM_old
LOS_Rate = LOS_Delta.VectorLength()
# range closing rate
Vc = -LOS_Rate
# Now, calculate the final lateral acceleration required for our missile
# to home into our target.
latax = RTM_new * N * Vc * LOS_Rate + LOS_Delta * Nt * ( 0.5 * N )
# Update mutable position objects so we can integrate forward to next frame.
msl_pos_previous = math.Vector3( msl_pos )
tgt_pos_previous = math.Vector3( tgt_pos )
# my job is done, it's now up to EXFLINT.Integrate() to steer the missile.
return True
Video Demonstration and Wrapping it All Together
The augmented PN (APN) formula above should always be used for any moving targets-- even non-maneuvering aircraft should have upward one-g sensible acceleration in a proper simulation environment, necessitating the need for APN.
The advantage of using APN guidance as compared to classic PN is that the commanded lateral acceleration (latax) is initially high but falls as the missile approaches the maneuvering target. Watch the YouTube video accompanying this blog post very closely-- you'll see that APN guided missile initially makes very violent maneuver to snap itself onto the collision path, then only minor adjustments are made just prior to missile impact. This is how optimal PN is implemented in the real world and how it should be done in realistic combat simulation games.
In the next (near future) tutorial, we will go over advanced guidance laws using theories of optimal control, which are derivatives of PN with more engagement information fed in, such as estimated time-to-intercept; and missile-target range. Feel free to message me on ModDB or YouTube if you have any questions or comments about implementing PN in your game environment.
YouTube HD Link: youtu.be/Osb7anMm1AY
From my last blog post, I've posted a demonstration of implementing Predictive Guidance (PG) in game environment. In that blog post, one of the things mentioned was the importance of Time to Go (TGO) variable in the homing loop. Just what exactly is TGO and why is it important? Easy question but turns out it was a bit harder than I thought to solve..
Time to Go (TGO)
TGO just as its name speaks for itself, stands for estimated "time to go until intercept". Basically, it's the fancy TOF counter that counts down to 0 when you watch Hellfire kill videos. In missile guidance parlance, TGO opens you up to many many more advanced guidance laws. If you think about it, TGO is the single important number which can express the geometry of the engagement.
As discussed in the previous blog post, having an accurate TGO is very important to achieving good homing performance. If TGO is inaccurate, you could actually have significantly higher miss distance than classical homing methods that you might as well not bother. Higher miss distance means, further correction efforts your missile has to commit to, thereby rapidly draining down energy and lowering the chance of a successful intercept.
How to not estimate TGO
Getting a good estimate of TGO ended up being a bit of challenge. If you think about TGO from elementary and rudimentary perspective, one could just say "range to target divide by speed = time left to go". The obvious problem with this statement is that both the missile and the target are never constant speed objects, they're accelerating more or less unpredictably.
Other more funnier proposals included, solving quadratic equations to obtain time-to-intercept, or even using a trajectory equation to estimate the time of flight. In fact, the sample code from my last blog post used the trajectory equation to estimate TOF:
# Estimate Time to Go (tgo) using trajectory equation.
# self.IMU_Measured_VR is the current speed of the missile as measured by
# Inertial Measurement Unit (IMU)
v_tgo = EXFLINT_Trajectory_ComputeTOF( 2 * range_to_target / self.IMU_Measured_VR )Both of these estimations ended up being a comedy. While above estimation resulted in several successful intercepts against slower moving aircraft in the last blog's video (actually in one of the scenes, the missile missed), when engagement was made against high speed targets (like supersonic cruise missile), homing performance went down the crapper to unacceptable levels -- more or less it hit about 2 out of 5 times against high speed targets. Test performance against ballistic missile targets resulted in kill ratio of zero.
The problem of above estimations is that they assume constant speed and that target and the missile are not accelerating. Missile's speed constantly changes throughout its flight envelope -- it accelerates to peak speed, then slows down as it coasts. Accurate estimation of TGO and engagement geometry requires solving nonlinear missile and target equations ahead of time.
How to better "estimate" TGO
Solving nonlinear equations of missile and target flight envelopes is way beyond the scope of math I wish to think about and is too overly complicated. Instead, we need find a much simpler method.
As it turns out, a great reference to this question is "Tactical and Strategic Missile Guidance" by Paul Zarchan; in one of his documents, he states: "the predicted intercept is calculated in flight by rapidly integrating the nonlinear missile and target equations forward in flight at each guidance update".
The keywords here are "integrating" and "at each guidance update." Ah, integration! When we're integrating, that means we only need to deal with 'at each guidance update', or more or less need to find an accurate instantaneous TGO that corresponds to concurrent target & missile's relative velocities. Turns out this happens to be very easy. No need for all that strange math porn!
To estimate TGO at each integration update, one could argue:
Tgo = Rt / abs(Vc)
Rt = relative distance (displacement) between missile and the target
Vc = closing velocityRt is the relative distance, or in other words, the displacement vector between the target and the missile at the time of calculation. Vc is the closing velocity.
Closing Velocity
Closing Velocity means "range closing rate" -- it is the rate at which the relative distance between the missile and the target is being closed, or the rate at which it is being "shortened" as the two objects are closing at each other. Relative distance is the distance (displacement) between missile and the target.
So to express closing velocity in integration terms:
Vc = ( Rt0 - Rt1 ) / dT
Rt0 = relative distance between msl & target at T=0
Rt1 = relative distance between msl & target at T=1
dT = time elapsed between measurements made for Rt0 and Rt1
Note that Vc is a negative numberSo we can argue that the distance left to go (relative distance, aka "Rt") divided by the rate at which we're currently closing that distance (Vc), equals our instantaneous Time to Go. Very simple solution to a complex problem! Integration ftw.
Putting TGO to work
Recall from my last blog post that at each guidance update, acceleration shall be proportional to Zero Effort Miss (ZEM) and inversely proportional to the square of Time to Go:
Required Acceleration = N * ZEM / Tgo^2
N = navigation constant (3 to 5; I use 3)
ZEM = Zero Effort Miss
Tgo^2 = time to go squared
Zero Effort Miss (ZEM) is expressed as:
ZEM_y = y1 + yt * Tgo
y1 = vertical (y-direction) separation between missile and target
yt = derivative of y (relative velocity)
Tgo = time to go
# Or more colloquially:
ZEM = Rtm + Vtm * Tgo
Rtm = missile-target relative position
Vtm = missile-target relative velocity
Tgo = time to go
Final Python code in FLINT missile script for AIM-120 AMRAAM:
# Navigation constant
Biased_NC = 3.0
# Integrate missile-target data
try:
self.rt_prev_frame
except NameError, ValueError:
# first frame initialization; IMU speed is safe here as missile hasn't accelerated yet
self.rt_prev_frame = range_to_target
Vc = -self.IMU_Measured_VR
else:
# at each integration update, we compute Tgo;
# EXFLINT_TICKTOCK is simulator update constant (dT)
Vc = ( range_to_target - self.rt_prev_frame ) / EXFLINT_TICKTOCK
self.rt_prev_frame = range_to_target
# Compute Time to Go
try:
v_tgo = range_to_target / abs(Vc)
except ZeroDivisionError:
raise EXFLINT_GuidanceLoopError(167)
# Compute required acceleration command
latax = LOS_new * Biased_NC * ( ZEM / ( v_tgo * v_tgo ) ) + LOS_Delta * ( Biased_NC / 2 )
Demonstration
Here is the concluding demonstration of the new homing performance by AIM-120 after applying the new Tgo estimation as described above. Is the homing performance any better? I surely think so, but you be the judge!
Had some interesting tech discussion with a buddy of mine and the discussion revolved around WiC MW's portrayal of ballistic missiles and the authenticity of battle space. "Battle space" in missile defense parlance, is the altitude/distance (kinematic space) and the 4th dimension, the "time" which defenders have to detect, track and engage an incoming missile.
The higher altitudes your SAMs could go, the bigger your battle space is. This is evident in history of interceptor development -- from the Reagan's SDI ("Star Wars") days, the endo-atmospheric rocket-based kinetic interceptor experiment was called "FLAGE (Flexible Lightweight, Agile, Guided Experiment)". After a successful demonstration of hit-to-kill concept with FLAGE in 1987, the SDI project moved to put this concept into practice, and a new project called ERINT (Extended Range Interceptor) was born.
Right from then in the later years of SDI during 1980's, the new paradigm shift in missile defense development was to "increase" the battle space -- intercepting targets in high altitudes gives you two benefits: (1) debris mitigation -- especially very important for chemical-bio payloads; and (2) more battle space means you have more opportunity to intercept, if first attempt fails. The "ERINT-1" prototype missile specified a much higher 28km intercept altitude, aided by low-noise seeker and 180 side thrusters to provide agility. Fast forward to 1994, the "ERINT" technology concept was chosen to become what is now known as the PAC-3 missile segment (yes, PAC-3 missiles are vastly different than the PAC-2 missiles and share no family lineage whatsoever; PAC-2 is the original Patriot missile, PAC-3 is SDI/Star Wars ERINT missile).
WiC Environment
In WiC, playfields are vastly small so we have to downscale a lot of things. Maps are only 1500 meters by 1500 meters maximum, which means, diagonally speaking, the maximum point-to-point distance you will have in game is about 2000 meters or so. So rather than calling these meters, we just call them "wic meters" or 'wm', because of the down-scaling we have to do.
One interesting feature in WiC and Ground Control EX3D world is that while playfield is limited, the game's skybox is virtually unlimited. It takes about 230km of draw distance before the game quits rendering the sky. This virtually unlimited sky box meant that ballistic missiles and anti-ballistic missiles could be portrayed with significantly less down-scaling than ever before, making the engagement feel more realistic.
Basics about Ballistic Missiles
Ballistic missiles really work in orbital and ballistic mechanics. In the simplest form, they are no different than throwing a stone up in the air and aiming it so it lands on the right spot. But since they are "missiles", they have guidance systems that make sure that the missile continues to point to the right launch angle until its booster burns out. Once it's in the space, it's total free fall. We will refer to the 'apogee' of the flight as Peak Altitude below.
Missile Data in WiC
So here is some data about ballistic missiles in WiC and their relevant speeds, altitudes, etc. Note that "wm" stands for 'wic meters' -- meters portrayed in WiC's down-scaled world.
- SS-21 Scarab (9K79 Tactical Missile Complex Tochka U):
Peak Altitude: 4,705 wm (equivalent to about 47-50km in real life)
Re-entry speed (speed at atmospheric ceiling interface): ~Mach 4.9 - 5.0
Terminal velocity at impact: ~Mach 3.3 - MGM-168 ATACMS:
Peak Altitude: 4,476 - 4,650 wm (equivalent to about 44-49km in real life)
Re-entry speed (speed at atmospheric ceiling interface): ~Mach 4.9 - 5.0
Terminal velocity at impact: ~Mach 3.1 - 3.3 - SS-26 Stone (9K720 Iskander M):
Peak Altitude: 5,095 - 5,680 wm (equivalent to about 50-56km in real life)
Re-entry speed (speed at atmospheric ceiling interface): ~Mach 5.7 - 7.1
Terminal velocity at impact: ~Mach 3.3 - 4.4 (depending on terminal maneuvers)
Note that terminal velocity is slower than re-entry speed -- yes, this is because FLINT engine in WiC actually simulates and calculates atmospheric pressure (drag), decelerating the missile as it negotiates atmospheric pressure at lower altitudes.
You can see that Iskander M comes with highest speed and the most devastating performance of all. Its terminal velocity has the greatest variance, because it throws 10-20G lateral maneuvers while it's coming down at Mach 6+, in order to make interception more difficult. This slows down the missile and exerts great deal of energy loss -- finally, missile then locks onto IR signature and tries to hit a moving target -- another huge G's it has to pull.
Interceptors in WiC:
Let's take a look at counter defenses in WiC for ballistic missiles now:
- PAC-3 MSE:
Maximum intercept altitude: ~3,216.2 wm (equivalent to about 32km in real life)
Typical intercept altitude: ~900 - 2,800 wm (equivalent to about 9 to 28km in real life)
Maximum speed in game: ~Mach 3
Maximum defended footprint size: ~2.25 kwm^2 - PAC-2 GEM-T:
Maximum intercept altitude: ~2,200 wm (equivalent to about 22km in real life)
Typical intercept altitude ~450 to 1,800wm (equivalent to about 4.5 to 18km in real life)
Maximum speed in game: ~Mach 3
Maximum defended footprint size: ~0.42 kwm^2
Based on these factors, it takes on average of about 14-17 seconds for PAC-3 missile in game to fly out of the launcher and reach its target at about 2,200 wm altitude. ~15 seconds is very realistic feel in portraying missile defense engagement times, as it is also about the same time it takes for a real-life PAC-2 missile to intercept a ballistic missile target at low altitudes. Engagement times could last for as long as 20-30 seconds in real life, but 15 will do for us in WiC.
Some interesting facts for missile defense system in game:
You'll note that sometimes you'll see a flash "bang" effect when a PAC-3 hits something in the high altitude, but sometimes you don't see anything (yet you know target got intercepted b/c your TA/score just went up). When a target gets intercepted and you don't see the "flash", the interception had likely occurred above 2,100 wm height. Particle effects do not draw at distances longer than 1,500 wm. If you see the flash, but it seems very high, then the target got intercepted at around 1500-1900wm, which it would still be traveling extremely fast (pretty much close to reentry speed with some deceleration).
The "TLL" parameter you see next to TBM count in Patriot message display stands for "Time to Last Launch" -- the amount in seconds the system has to launch its interceptors, in order for them fly up there and hit the target before it becomes unengageable. "Unengageable" means, the target has breached the minimum altitude distance, where it is now impossible to intercept geometry-wise.
Sometimes you'll see a ballistic missile coming down with TLLs decreasing pretty fast (i.e. 13s then 12s, 9s, etc) -- it's probably an Iskander coming down at Mach 7. Or, sometimes you'll also see the rate of "TLL Drop" suddenly slow down or reverse itself where it increases -- this can be caused by one of two things: either (1) the ballistic missile has hit the atmospheric ceiling and is decelerating quite hard due to drag; or (2) it is probably an Iskander that's currently pulling 20G lateral maneuvers, burning energy and slowing down its free fall in the process.
When TLL reaches negative (number turns to red), no more interceptors can be launched -- if the existing interceptor already launched misses its target, it's now considered a "leaker" and no further intercept attempts can be made.
Cruise missiles are essentially unmanned aircraft (just without recycle feature). For accurate portrayal of such weapon for World in Conflict, we need to make sure they use a set of navigation waypoints, flying low (at height of between 25 to 50 ft) and evading radar detection.
We would prefer that the cruise missiles use fly around the edges of the map, preferring to avoid contact with enemy and maintain the element of surprise for as long as possible -- at the expense of missile taking much longer to arrive on its target.
In order to program such artificial intelligence into the system for navigation, we use Shortest Path First implementation utilizing Dijkstra algorithm. Every waypoint known in game map is a "node", and distance to every node is known and calculated, to dynamically calculate a flight plan based on the least amount of total "link cost" across the entire path. Come to think of it, Dijkstra algorithm is also very popular with internet routers for calculating shortest paths on network's Interior Gateway Protocol (IGP) topology.
def Generate_Waypoints( self ):
global nodes
"""
RGM-109E Tactical Tomahawk for WiC MW
En Route Navigation for TERCOM mid-course guidance
Rather than running straight to the target and have everyone
and their grandmother shoot at the Tomahawk, we'd prefer the
missile to fly low and sneak around on the sides of the map,
using a set of waypoints. It will take longer to get there,
but it allows the Tomahawk to minimize radar detection and
maintain the element of surprise.
Calculate the shortest 2D world waypoints (X, Z) for the
cruise missile to navigate thru to approach the terminal
acquisition area (kill box). Upon arrival, missile will
need to transition from en-route control (mid-course) to
terminal guidance, pitching up to about 100wm height and then
diving onto the target.
1500 +------------------+--------------------+
| (*7) Delta (*6) Charlie (*5) |
| 1490,0,10 November 1490,0,1490 |
| 1490,0,750 |
| Grid | Grid |
| D | C |
| | |
X 750 +-(*8) Whiskey-----+----------Echo (*4)-+
axis | 750,0,10 | 750,0,1490 |
| | |
| Grid | Grid |
| A | B |
| 10,0,750 |
| 10,0,10 Sierra 10,0,1490 |
| (*1) Alpha (*2) Bravo (*3) |
0 +------------------+--------------------+
750 1500
Z axis
Navigation nodes
alpha: 1 sierra: 2 bravo: 3 echo: 4
charlie: 5 november: 6 delta: 7 whiskey: 8
Implement ECMP routing for salvo fires against target grids
having equidistant paths?
"""
INAV_MAX_COST = 32768
def SPF(graph, start, end, visited=[], distances={}, predecessors={} ):
# Dijkstra Shortest Path First (SPF) Algorithm
# Credit to/courtesy of: http://rebrained.com/?p=392
# First time init
if not visited: distances[start]=0
# Terminal node: find path to it and return
if start==end:
path=[]
while end != None:
path.append(end)
end=predecessors.get(end,None)
return path[::-1]
# Process adj nodes and keep track of predecessors
for neighbor in graph[start]:
if neighbor not in visited:
neighbordist = distances.get(neighbor,INAV_MAX_COST)
tentativedist = distances[start] + graph[start][neighbor]
if tentativedist < neighbordist:
distances[neighbor] = tentativedist
predecessors[neighbor]=start
# adj nodes processed, mark current node as visited
visited.append(start)
# Find the closest unvisited node to the start
unvisiteds = dict((k, distances.get(k,INAV_MAX_COST)) for k in graph if k not in visited)
# Get the minimum key in dict unvisiteds
# This method requires python 2.5+... WiC cpython uses 2.4:
# closestnode = min(unvisiteds, key=unvisiteds.get)
#
closestnode = min([ (unvisiteds[x],x) for x in unvisiteds ])[1]
# Now take the closest node and recurse, making it current
return SPF(graph,closestnode,end,visited,distances,predecessors)
nodes = {
1: math.Vector3( 15, 0, 15 ),
2: math.Vector3( 15, 0, 750 ),
3: math.Vector3( 15, 0, 1485 ),
4: math.Vector3( 750, 0, 1485 ),
5: math.Vector3( 1485, 0, 1485 ),
6: math.Vector3( 1485, 0, 750 ),
7: math.Vector3( 1485, 0, 15 ),
8: math.Vector3( 750, 0, 15 )
}
# Get the nearest ingress & egress enroute waypoints for missile
# launch location and desired target coordinates (terminal basket).
start_max_dist = INAV_MAX_COST
end_max_dist = INAV_MAX_COST
for i in nodes:
len_to_start = ( math.Vector3( self.current_state ) - nodes[i]).Length2D()
len_to_end = ( math.Vector3( self.PN_Terminal_Basket ) - nodes[i]).Length2D()
if len_to_start < start_max_dist:
start_wp = i
start_max_dist = len_to_start
if len_to_end < end_max_dist:
end_wp = i
end_max_dist = len_to_end
# SPF link path costs; IGP adjacencies
graph = {
1: { 2:7, 8:7 },
2: { 1:7, 3:7 },
3: { 2:7, 4:7 },
4: { 3:7, 5:7 },
5: { 4:7, 6:7 },
6: { 5:7, 7:7 },
7: { 6:7, 8:7 },
8: { 7:7, 1:7 }
}
self.ENR_waypoints = SPF(graph, start_wp, end_wp)
return True
Implementing the Command to Line of Sight (CLOS) guidance method in World in Conflict (also can be ported to other game environments).
YouTube Video:
Link - Youtube.com
def GCFLINT_Command_to_LOS( msl_pos, launcher_pos, tgt_pos, latax, cre_data, beam_motion_data ):
"""
Command to Line of Sight (CLOS) Guidance
msl_pos = (Vector3) missile's current position
launcher_pos = (Vector3) launcher's current position
tgt_pos = (Vector3) target's current position
latax = (Mutable Vector3) mutable object for providing guidance command
cre_data = (Mutable dict) dict object for Kalman estimation states on CRE
beam_motion_data = (Mutable Vector3) mutable object for recording previous
beam motion
Command to LOS (CLOS) Guidance or "three point guidance" is probably the
oldest and the first rudimentary form of missile guidance methods.
Tracing its roots back to the Nazi Germany's Wasserfall experimental SAM
and early forms of anti-shipping guided PGMs, it was originally conceived
as Manual Command to LOS (MaCLOS or MCLOS), where a human operator
remotely steered the missile along his visible line of sight toward the
target.
After the World War, MCLOS was further modified with improvements in
sensors and analog computing technology, spawning new derivatives such as
Semi-Automatic Command to LOS (SACLOS), Automatic Command to LOS (ACLOS or
simply CLOS) and Beamriding Guidance. In case of SACLOS, the operator has
to maintain his sight on the target and the guidance computer will
automatically generate the necessary steering commands to the outgoing
missile -- a good example of this is BGM-71 TOW missile. Fully automatic
CLOS (ACLOS) was used on first generation SAMs (i.e. Talos, Nike Zeus, etc).
Even to this day, ACLOS is widely popular for cheap short-range AA uses
(i.e. SA-22 Pantsir/SA-19 Tunguska, Crotale, RBS-70, Roland, etc), because
the missile is very cheap to manufacture (there is no need for seeker and
complex embedded electronics).
CLOS works on the premise that the target, outgoing missile and the launcher
are all on the same Line of Sight (LOS) line. As missile is outgoing, the
guidance computer on the launcher will steer the missile to snap it on its
sightline/LOS toward the target.
The outgoing missile's distance normal to the launcher-to-target LOS (that
is, how far the missile is off from the LOS line) is known as the
'Cross Range Error' or 'CRE'. It is this 'CRE' that the guidance computer
will have to reduce to zero in order to get the outgoing missile to snap
back on the LOS line toward the target. CRE is to be calculated as follows:
CRE = |radar_to_missile| x<cross product> |radar_to_target|
-----------------------------------------------------
|radar_to_target|
The guidance computer will calculate the required lateral acceleration to
bring CRE to zero, where:
required acceleration = K * CRE + Beam_Motion_Term
K = optional Guidance Gain
Because CLOS relies on the launcher-target LOS as its principal tracking
reference, it is quite vulnerable to high velocity situations, especially in
situations where the target is crossing; in such cases, it can behave as bad
as pure-pursuit/tail-chase homing guidance. To help mitigate the increased
acceleration requirements against crossing targets, a "Beam motion" term is
added after the guidance command. Beam motion is the target's acceleration
normal to the launcher-target LOS.
Addition of beam motion term allows CLOS missile to more quickly react to
changing LOS rate, but ultimately, CLOS is at best, good for producing lot
of cheap anti-aircraft and anti-slow-moving (i.e. tank) missiles. For
intercepting high performance targets with good accuracy, or to achieve
sophisticated "hit to kill" type of interception, you would want to use one
of the modern derivatives of Proportional Navigation (PN) family of
guidance methods.
"""
import wic.common.math as math
from predictorFCS_flint__includes__ import EXFLINT_Kalman_Filter
launcher_to_msl = math.Vector3( msl_pos ) - launcher_pos
msl_heading_direction = ( math.Vector3( tgt_pos ) - msl_pos ).NormalizeSafe()
command_los = math.Vector3( tgt_pos ) - launcher_pos
# Cross Range Error (CRE) -
# radar_to_msl <X cross product> radar_to_tgt * ( 1.0 / radar_to_target )
CRE = EXFLINT_Kalman_Filter( cre_data, ( launcher_to_msl.Cross(command_los) * ( 1.0 / command_los.Length() ) ).Length() )
# Beam motion term -- perceived target's inertial acceleration normal
# to Line of Sight
Bmp = math.Vector3( tgt_pos ) - beam_motion_data
beam_motion_data = math.Vector3( tgt_pos )
# Now, calculate the final Lateral Acceleration required for our missile
# to home into our target.
latax = msl_heading_direction * CRE + Bmp
# my job is done, it's now up to EXFLINT.Integrate() to steer the missile.
return True
The Story of World in Conflict MW Mod
The Beginnings: Air and Support Roles in WiC
Initially, WiC had a simple arcade battle concept of rock-paper-scissors. The most powerful role of World in Conflict is arguably the Air role. Even though Air cannot capture nor hold the ground, its high mobility meant that an air player could set the terms of the battle, forcing the defenders to respond when and where he chooses.
This phenomenon was clearly noted during ESL and CPL professional league games between 2007 and 2009. The fact that Air player sets the tempo of the battle and acts as a primary TA generator for his team speaks volume about the role's powerful capabilities in the game.
However, in order to balance the game, Air's real power projection capabilities have been limited to very short, within face-to-face ranges. Likewise, air defense units also have such smaller ranges. Against a seasoned air player, Air defenders (support players) must maintain a passive posture and focus on setting up a wide area net of short range AA units. Spacing of AA units is critical, so that when one area is breached, AA units from nearby locations can quickly move in and reconstitute air defense at the breached sector.
Although the developers have simplified the Air power in game for balance reasons, they did however score well when it comes to portrayal of realistic doctrines - throughout history of warfare, anti-aircraft defenses have been passive by nature and air power always held the initiative. It is said that the best counter to enemy aircraft is another aircraft. Ground-based air defenses from the days of WW I had always strategically failed when no friendly aircraft were available to help them.
Fun Mod (pre-MW Mod) and Enlarged Air/Support Fire Ranges
During the early versions of MW Mod (formerly known as Fun Mod), air units had their range of fire increased from that of the vanilla game. The balancing problems were obvious. Even though air defense units also had their ranges increased with introduction of Heavy SAM units, the increased stand-off capability of the Air role had given support players a very stressful situation when dealing with a real human air player on the opposing team.
The increased stand-off range of Air role in Fun Mod meant that air player could hide and surprise the opposing player with pop-up attacks. This gave little to no warning to the defenders, and required the support player to rapidly predict the air player's next moves. Paranoia was natural when playing support.
Despite this, a skilled support player could very well manage and still control the battlefield. The game effectively became a ‘hide and seek' situation between air and support players, with both sides constantly predicting each other's moves.
From Fun Mod to MW Mod: Firepower Madness
When Fun Mod transitioned to MW Mod beta, numerous enhancements in gameplay had created new challenges for balancing in multiplayer matches between online players. There was one dramatic game changer - cruise missiles. Now the game introduced automatic robotic units that auto-pilot themselves into suicide and then blowing themselves up once closing on their targets.
Previously, with increased stand-off fire range of the Air role, a paranoid support player could deal with an air player on one-off basis - one support player could deal with one air player. However, with cruise missiles, things have changed dramatically to a new level that would draw the blueprint for MW Mod's future developments.
Cruise missiles by nature fly extremely fast. During multiplayer games, it took the attention of an entire team to shoot down or evade a single cruise missile. The high speed of cruise missiles allowed the air player to quickly apply firepower to anywhere on the map without having to risk his own helicopters - effectively a big artillery. This also allowed the air player to punch through enemy AA belt by attacking the air defenses themselves. Short range AA guns could shoot down the cruise missile, but became vulnerable to saturation attacks.
Heavy SAM units were given a new offensive special ability that gave them highly agile homing missiles to take out fast moving targets like cruise missiles. This required the support player to manually target the cruise missile. Even then, cruise missiles still consistently made onto their targets - the tail-chasing nature of the homing missile caused even the high-speed SAM to lag behind the cruise missile. By the time a SAM could intercept the cruise missile, it would have already struck its target.
But all of this talk is relevant to defending from a single cruise missile. It became painfully obvious that air players would employ saturation tactics to simply bulldoze the entire opposing team. Human support players were simply unable to react fast enough to manually identify and target incoming cruise missiles in time. At most all they could do was pop smoke and move out the way; some players simply disbanded their units when enemy cruise missiles became visible.
The problem of cruise missiles had forced us to re-evaluate their role in the game. As an interim measure, their prices had gone up substantially to the point that nobody used them anymore - they were effectively removed from the game until a better solution could be found.
Defeating the Vampires - PythonShooter h4x
At the time when cruise missiles were introduced, numerous capabilities of WiC's PythonShooter have been discovered. Instead of just firing projectiles, the PythonShooter could be used as an API to fool the game into doing many more things. The improvements made in working with PythonShooter had allowed us to figure out a robust solution to the cruise missile problem.
The idea was simple: if the cruise missiles were to remain in game, they would have to be countered. It was obvious that the reaction time, firepower and operational availability of existing AA units did not match the advancing air & missile threats.
With this in mind, the first ambitious work using PythonShooter was to develop an Integrated Air Defense System (IADS) in an RTS game, with conceptual ideas borrowed from the US Navy's Aegis Combat System. Reduction in reaction time through automation and computer-aided command and decision process for the support player became the primary goals.
The new IADS was programmed in Python with an exact scenario of saturation air and missile attacks in mind. Once activated by the player, the automated program immediately identified the incoming air and missile threats as hostile and assigned each a priority of destruction. From that point on, the computer was completely on its own, free to fire on its electronic will at anything diagnosed as a threat. Once the IADS is "weapons free", support player is detached from the entire process - the human players can now focus on what they do best in WiC - strategize their next moves, while the computer deals with the ongoing chaos of incoming enemy air & missile attacks.
Integrated Air Defense System (IADS) Development
The development of IADS for WiC was the most protracted and ambitious project in the entire MW Mod development history. The goals were ambitious for a mod with just one person doing most of the development work - World in Conflict would have to become the first casual game in history to fully simulate a working IADS, with fidelity rivaling those of air combat simulation titles.
In addition, ease of use was a must - support player must be detached from the technical mumbo jumbo, while maintaining a high degree of realism. A fine balance had to be achieved, where a casual player without any knowledge of military technologies would enjoy the game, while military technocrats would appreciate the authenticity and degree of realism delivered by the game.
All of this effort just to make sure cruise missiles stay in the game - some in the community had suggested that cruise missiles simply be removed altogether rather than spending protracted development time on IADS. Instead, they argued that it would be a much better use of our time to add new models, new units, new tactical aids (like hydrogen bomb, more nukes), etc.
However, the counter-argument was that MW Mod would bring "nothing new" to the table if we just keep adding new units that would all behave the same (a tank shoots a vehicle, a helicopter kills a tank, what else?). I was adamant that MW Mod should try bringing realism in a different direction - a direction where no strategy games have ever gone to in the past. Of course, there is the old saying "if you are not being criticized, you may not be doing much." Controversy amongst those in the small WiC community regarding the IADS development was something I had valued as a compliment.
The IADS development was started at the time when I had no experience whatsoever in Python. Coming from limited programming experience with C, Python was quite awkward. It took a while to get used to Python's object-oriented structured programming, but its ease of code readability made it lot easier to quickly learn and pick up the language.
New Discoveries
During the IADS development, lot of new discoveries were made surrounding how the World in Conflict's Server Game environment known as "WICG" (stands for WIC Game) works behind the scenes.
PythonShooter interface that Massive developers left behind was really the lucky shot that saved MW Mod from being abandoned.
Looking back, Massive devs would have never thought that PythonShooter would be used for activities other than shooting projectiles. Well, they inadvertently left a loophole and we capitalized every cent out of it - the IADS working through PythonShooter interface was being coded to act as a artificial intelligence system. Everything from target detection, tracking, classification and prioritization of targeting was being done by the IADS - activities far from simply ‘shooting projectiles.'
With these new discoveries, one of the new tricks I learned was sharing of information between different units across the game (data-link). This opened a pandora's box to all of future MW Mod developments.
The concept of data-linking developed for the controversial IADS so cynically called "overpowered, moditis-induced toy" was so versatile, that development of IADS had contributed to the future Fixed-Wing Aircraft system. Without IADS development, Fixed-Wing Aircraft would have been simply impossible.
Fixed-Wing Aircraft and Prelude to MW Mod 2 for World in Conflict
The development of IADS had produced new knowledge to proceed with the concept of fixed-wing aircraft system for WiC. However, the work was dead on arrival - I was adamant that fixed-wing air in WiC would look stupid under the existing game environment. In order to properly introduce fixed-wing aviation, we must first fix the underlying problem - the homing missiles.
If we were to introduce air force units into the game, the combat scenery would have to look beautiful - this meant that homing missiles used in game would have to be changed to use "lead-pursuit" guidance. Under the lead-pursuit homing, the missile would lead the target into a mid-air collision, rather than chasing after it. The resulting hit would look like something out of Star Wars.
Initially, the concept of revamping the homing guidance law of projectiles in WiC was deemed impossible and was considered the "holy grail" of WiC modding. It simply could not be done with the limited access that WiC SDK provided. However, during the development of IADS, it was discovered that the PythonShooter had an unintended write access to a player owned unit's EX_World (3D space) position coordinates. At first, this was thought as a game bug; but then it too quickly became a new opportunity for innovation.
Immediately, work was done to put the "EX_World write access phenomenon" to a test to study its feasibility. An Mi-24 Hind helicopter unit was given an experimental PythonShooter code that changed its EX_World position every frame. This resulted in the Hind chopper following the target in an automatic pursuit. A fat Hind helicopter had become a homing projectile!
After the test, an experimental project was started on the backburner - it was to be named Flexible, Advanced Air Interceptor, later re-named to simply "Flexible Interceptor" or "FLINT" for short.
Initial Development of Flexible Interceptor (FLINT)
The concept behind FLINT was actually not my idea. It was first suggested by DeltaWulf, one of the voice actors for the MW Mod team, back in 2009. His idea was to spawn a helicopter unit and create a mechanism that would automatically "drive" this unit without player's input.
However, this "mechanism" was the problem - just how do we do it? Well, with the discovery of "EX_World write access" phenomenon during IADS development in 2011, we finally found the solution to make his idea work.
A second problem rose during protracted FLINT development cycles. None of us had any working knowledge of math or rocket physics beyond the basics taught in high school and college courses. None of us had any idea on how a real-life missile "leads" the target. None of us had much idea in basics of linear algebra and working with vectors in general. This created an enormous challenge for FLINT development that almost killed the project. Never before, a hobby for gaming became as stressful as a day at work.
So, it was time for a crash course. Where the basic knowledge of linear algebra and mathematical concepts were lacking, Kahn Academy and YouTube came to the rescue. The next was learning how missile guidance systems work in real life - this was even harder. It quickly became obvious as to why missiles behave silly in most games - most game developers have no idea on how to do it, and neither did I.
During this time, an air combat simulation game by Eagle Dynamics (ED) known as Digital Combat Simulator (DCS) was very inspiring to the development of FLINT. The high fidelity and realism delivered by DCS in every respect only inspired me to go one step farther. Browsing through the ED forums, I've learned more knowledge about combat systems, but more importantly, the raw data and truth about those systems, rather than fanboyism, which the internet is full of. Particular attention was given to forum posts made by GGTharos.
Putting Knowledge to Work for FLINT
I have soon learned that many missiles in real-life use Proportional Navigation (PN), first developed by the US Navy during WW II, and first implemented on the AIM-9 Sidewinder in 1954.
Putting the concept of PN into mathematical formula is one thing - Wikipedia has that. Putting the concept and mathematical formula into a workable software code with limited math knowledge was completely another. You actually had to understand the meaning behind the math and physics involved between the lines - I didn't at the time. Google searches and books on missile guidance had produced nothing - many of them were written by academics and professors who use the same old mathematical jargon that noobs like me would never comprehend.
During the quest to understand missile guidance, I've run into Defense Technical Information Center (DTIC), run by the US Department of Defense. The DTIC archive is full of declassified military technical and scientific information that were cleared by the DoD for public release. Many of the archived and declassified writings publicized there were put together by those who practiced them, rather than being written by academics.
Studying through DTIC archives, a breakthrough in understanding of PN and the most basic principles of homing guidance have been made. On July 14, 2011, an experimental FLINT Python code using my new understanding of PN was put into action for the first successful guided intercept test. Again, ceremonially, we had decided to use the Mi-24 Hind helicopter model to represent the homing kamikaze missile for this experiment.
After much anticipation, the Hind unit was coded with target information and given the Attack order to initiate the test. It worked! - the Hind smoothly accelerated like clockwork and started leading the target as it flew, then collided with the moving target. Other mod team members on TeamSpeak and xfire watching this event had cheered in joy as history has just been made in World in Conflict modding.
World in Conflict is a game that was abandoned by its own publisher. Its own developers have their hands full working on new projects that they couldn't possibly help modders. All felt lost and WiC seemed hopeless to achieve portrayal of modern firepower. On July 14, 2011, the first successful guided intercept test of FLINT changed everything we knew about WiC. It was a historic day for World in Conflict as a game and changed the course of MW Mod development forever.
Recent Developments and Going Forward
With FLINT maturing and transforming the homing missiles in WiC, fixed-wing aircraft were quickly introduced. The introduction of fixed-wing air had completely changed the gameplay - even the old players who criticized the mod for whatever grievances they had were impressed.
What started as a humble Fun Mod with overly ambitious and tenacious goals had ended up into a full blown modern combat simulator for arcade-styled RTS genre - something no other game has ever achieved before.
Where do we go from now? Well, World in Conflict is a dead game. Ubisoft and Massive had confirmed to us that franchise has been killed and that there will not be a WiC 2. But bad news is always a time for new opportunity - the extensive knowledge we had gained developing FLINT meant that we could now port the entire system to another game. FLINT engine would go on; it just needs a new home.
However, the new challenge is that many game publishers are increasingly becoming uneasy toward community developers. I'd love to mod Battlefield 3 using FLINT tech, but unfortunately there are no plans to allow modding. Such is true with many other games.
Wargame European Escalation seemed to be another promising game, but it just didn't click with me. World in Conflict is still my favorite RTS. There is just one thing that other RTS games can't seem to figure out - the camera. In WiC, camera can freely behave to the point that you can play the game as if you're in a first person shooter. No other RTS games seem to have figured this out. I am however interested in the upcoming W-EE: AirLand Battle title from Eugen (but ofcourse, will they allow modding? Time will tell.)
We're also evaluating feasibility in modding for ArmA. ArmA has very extensive modding support and a very strong community. However, being new to a completely different environment, it would take a while to get used to. It may be easier to join an existing successful realism mod for ArmA (i.e. ACE) to provide whatever assistance I can on missile simulation.
With all of this said, until we find a new viable home for ourselves, WiC is still our most favorite RTS game and WiC MW Mod will continue on in incremental updates (even if we move onto another game) -- that is, until Ubisoft officially pulls the plug. As long as WiC lives, so will the MW Mod ;-)