Six more weeks have passed since I first posted about Adaptive Volumetric Meshes, which have since turned into Voxel Mesh Hybrids after some refinements for the sake of simplicity and ease of use. It's the driving tech behind the procedural and player-authored meshing that our game in production, NOWHERE (alpha available for download), requires.
After the recent refinements, it's time for another short write-up, as the work has reached a stable state and is nearly ripe for release as part of the next Alpha later this month. Beware: from here on it gets technical.
In this article I'm going to walk you through the construction of a complete voxel mesh hybrid structure including level of detail using an analog quadtree structure and an exemplary shape.
We're going to source a simple shape for the rasterization / tracing. In 3D, this could be a distance field, a volumetric texture, an existing high resolution mesh, basically any boolean spatial structure.
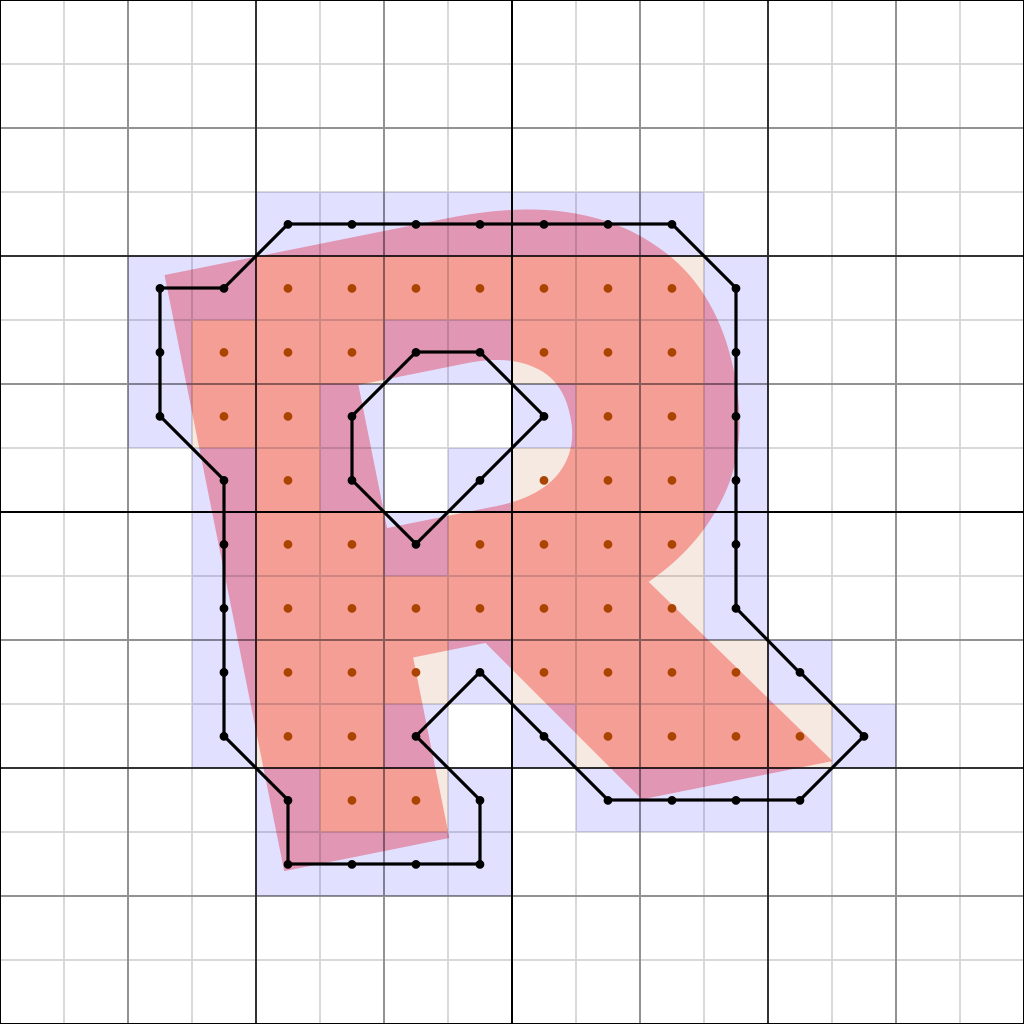
Now, for every voxel enclosing a part of the volume, we add a new cell to a single quadtree, along with its parent cells, at a preset homogeneous level of detail, in this case level 4, which equals a resolution of 16x16. Depending on the source data, there are two ways to construct the tree: top-down or bottom-up. In this case we're going bottom-up.
The data structure for voxel mesh hybrids is essentially just a 3D grid of cells in a fixed resolution, which can be stored in a sparse octree for memory efficiency (and additional perks, which I'll get to further below).
Each cell acts both as voxel and point, holding a vertex with coordinates relative to the extents of the cell, so that -1 -1 -1 is the lower left front, 1 1 1 is the upper right back, and 0 0 0 is right in the center of the cell. Note how all vertices here are still at their default locations. This isn't strictly necessary, but helps to understand the implicit connectivity step that comes next.
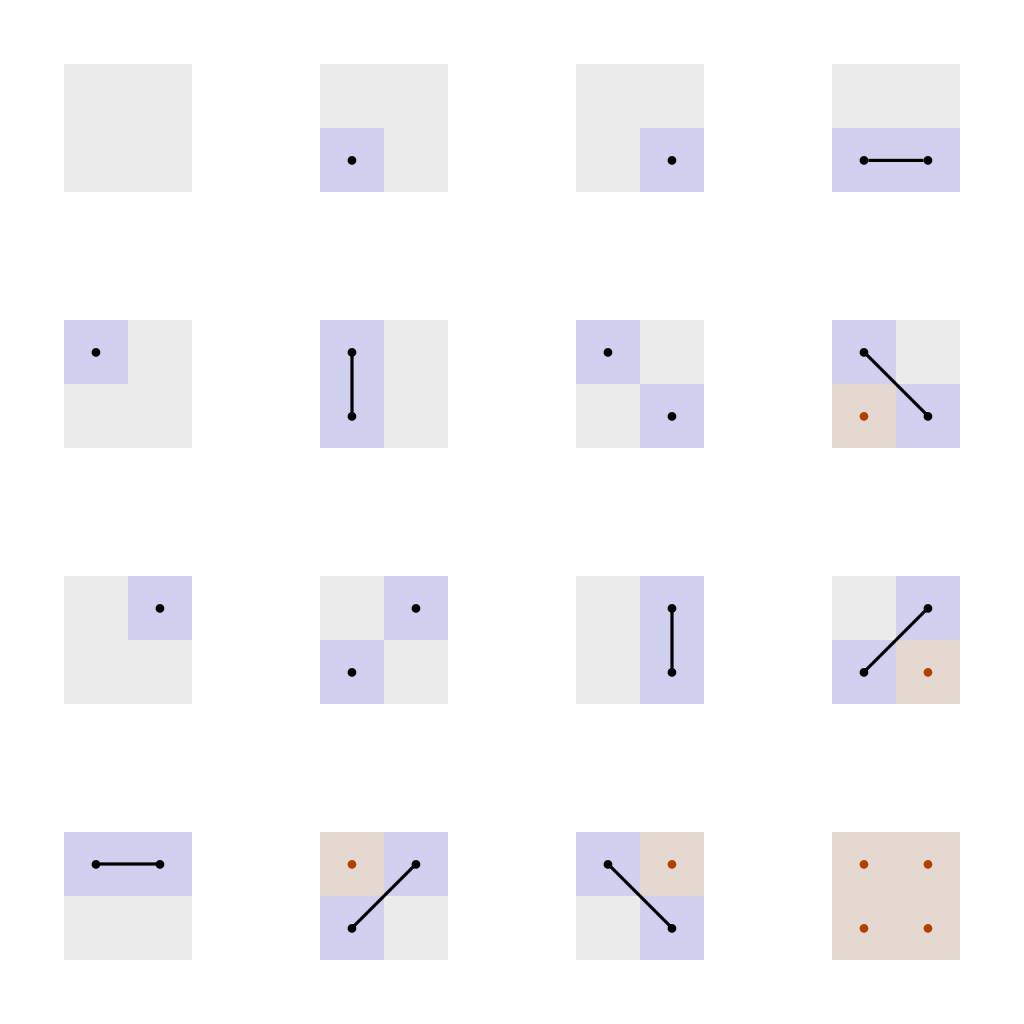
Using a simple set of 16 binary marching cube connectivity rules (in 3D, it's 256 different combinations), we now build a dual mesh, connecting 4 adjacent cells at a time. Thanks to the connectivity rules, the mesh is guaranteed to be watertight, non-intersecting and two-manifold.
As a set of adjacent vertices always results in the same creation of edges, connectivity is implicit: the resulting mesh can be regenerated as often as needed after changes and does not have to be stored permanently or queried for editing. Edges local to each vertex (in 3D, the 1-ring neighborhood) can be constructed ad-hoc from a cells surrounding Moore neighborhood (2D: 9 cell kernel, 3D: 27 cell kernel), which is useful for doing ray intersection tests, finding the vertex normal, checking if the vertex is degenerate, estimating curvature, vertex smoothing etc.
Furthermore, the marching cube has been extended with a bitmask marking inside cells, which helps to discern if a vertex is visible, and allows to easily find degenerate vertices. A degenerate vertex is any vertex with a valence < 2 (3D: degenerate if valence < 3 or ring loop hops counted != valence), unless that vertex is marked as inside.
As an additional step, it is possible to merge quadtree pairs which are completely inside into their parents, and resolve neighbor queries to the parent cell, but in our case we actually want to persist data in the volume, so we keep the cells around.
As a next step (which can be done independent of connectivity), we move vertices closer to the surface. In this case, the vertices were hand-edited, but this could also be automated using a distance fields gradient data; if the data source is already a mesh, the vertices would copy representative positions

Vertices on the surface have been moved to the boundary, reconstructing the surface. Note the oversampling at four locations caused by the coarse resolution.
If the data source is binary, a smoothing step could be applied, moving each vertex towards the average of its neighbors, which usually gives good results but doesn't preserve hard edges. Also, vertices may end up clamped against the cell boundary after several iterations. Applying some kind of constraint to keep the vertices close to the cell center is advisable.
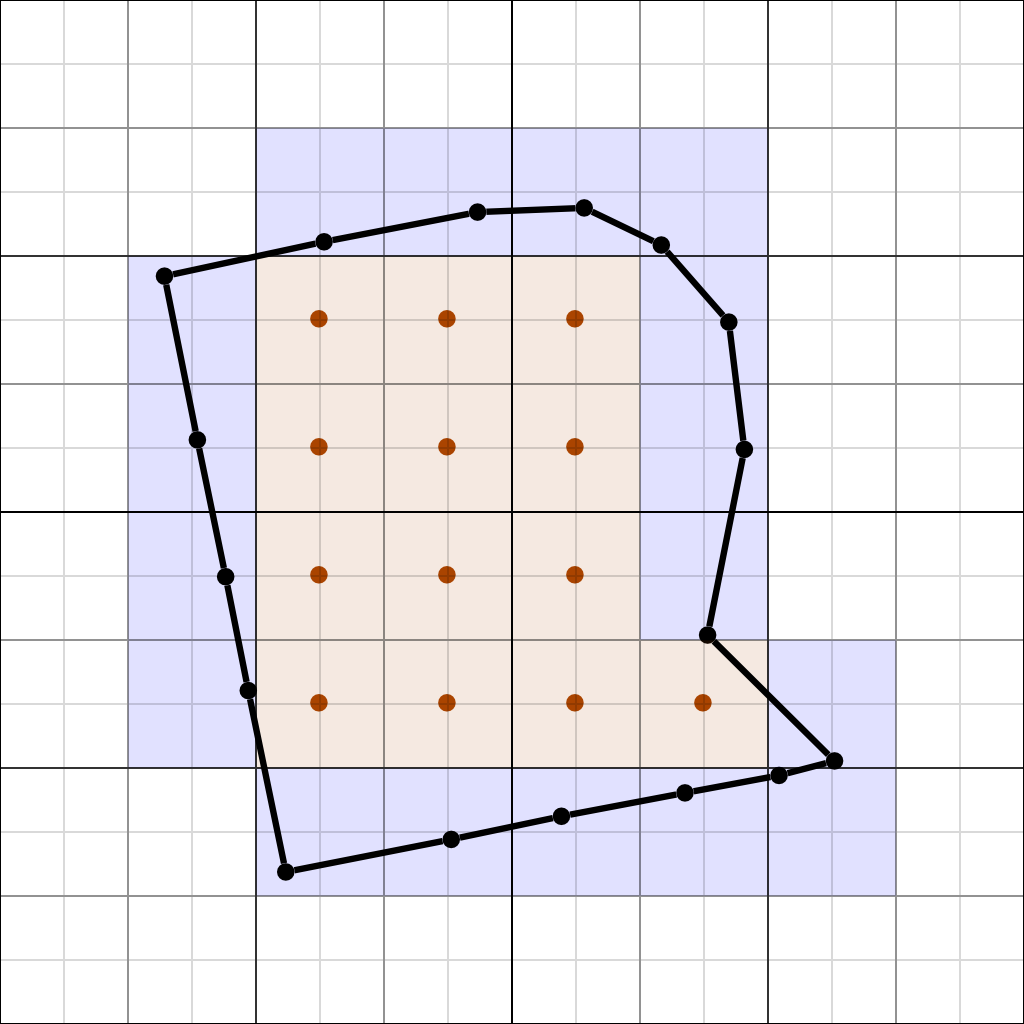
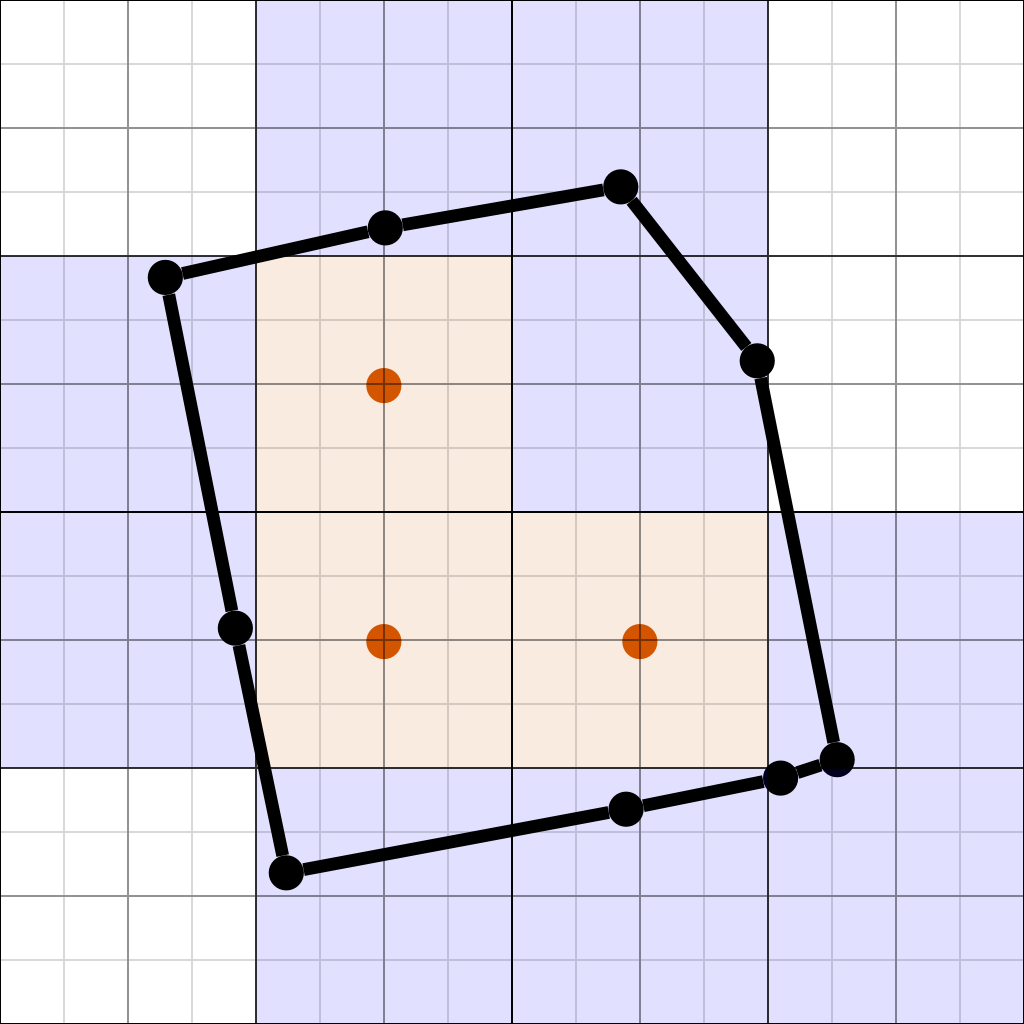
Since the parent cells are of the same structure as the leaf nodes, we can mesh the tree at lower levels and get coarser meshes with can be used for level of detail and building collision meshes for physics simulation. Therefore, we now adjust the vertices at level 3 so that their edges resemble boundaries around the vertices of level 4:

The level 4 cell structure and its implicit mesh.
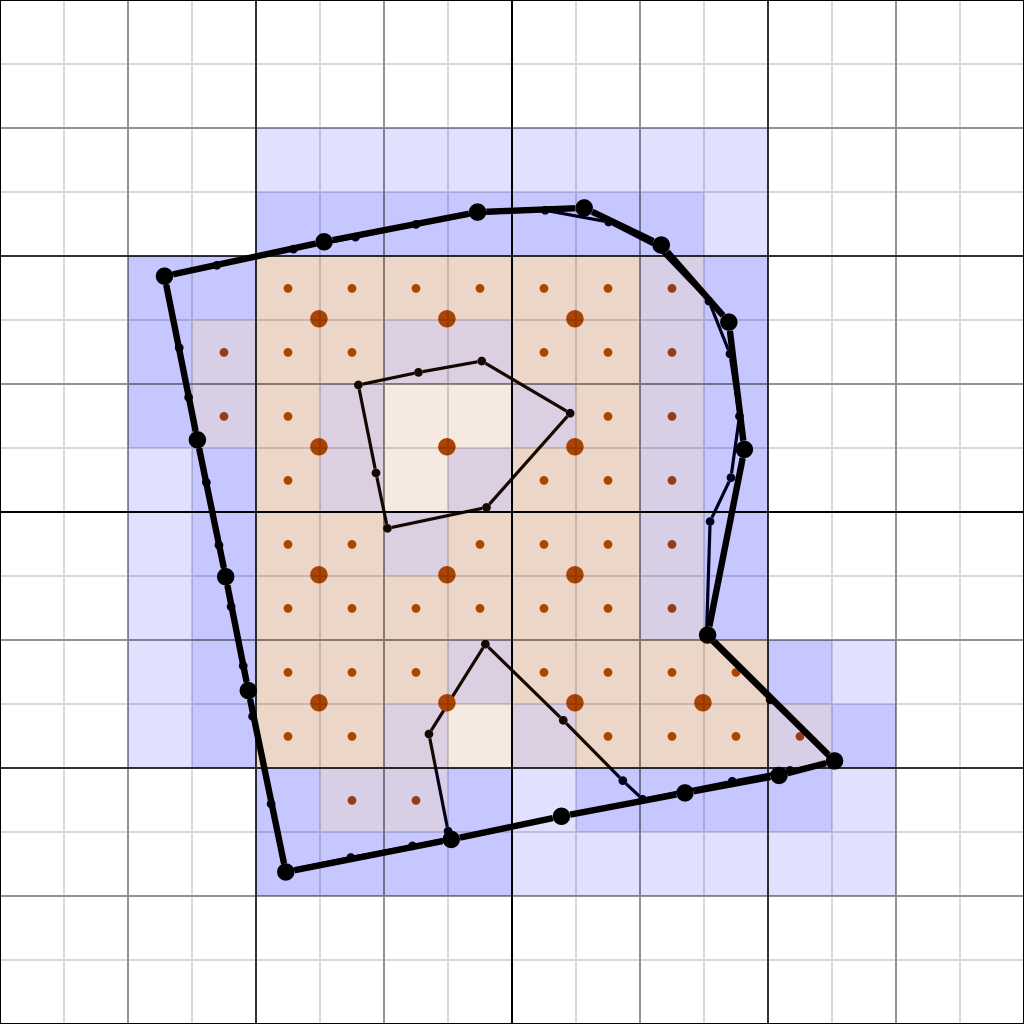
Level 3 cells superimposed over level 4, with outer vertices forming an implicit boundary mesh. The coarse resolution causes the concave sections to disappear early.
This process can be repeated up to level 1, building all levels of the mesh:
This concludes the walkthrough for the voxel mesh hybrid creation.
Voxel meshes can be edited with classical techniques available both to voxel and mesh editing, with differences in any task involving changes in edge connectivity, as with voxel mesh hybrids, connectivity is implicit: new triangles are only created when cells are removed or added. Variety in detail magnitude on a single level is possible up to a certain degree. Edge lengths may range from 0 to 2*sqrt(3)*(cell width).
Extrusion must be performed on the voxel level, with edge lengths dependent on how close vertices are to cell boundaries.
Subdivision must be performed uniformly, subdividing all cells to a higher level, testing against the vertex ring to decide where cells need to be created (only add new voxels whose boundaries collide with the lower level mesh volume), then projecting the new vertices to the surface.
So much for now. More to come.