In todays class we will study the equations of motion for a rotating sphere rolling and sliding on a surface, impacting on other speheres or surfaces or possibly sent flying in free fall all around the place.
You there in the back of the hall, don't fall asleep, this comes into your grades you now!
Consider the following case:
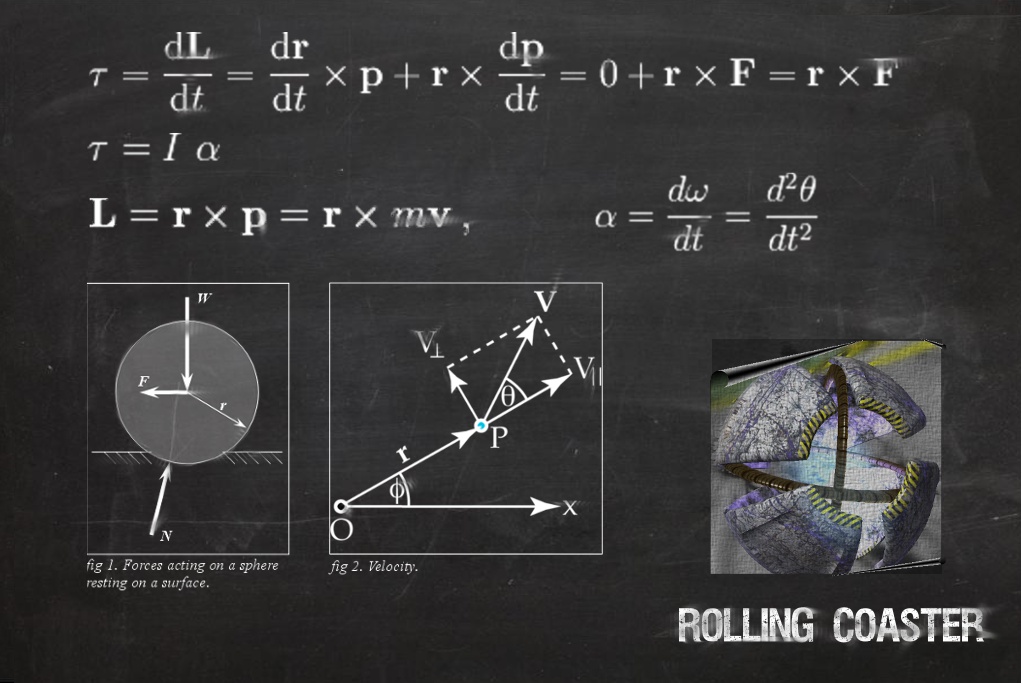
Where:
I is the moment of inertia (you will find it for any possible object in your Book of Equations, did you remember to bring it to class?).
F the accelerating force acting on the sphere
N is the force acting on the sphere by the surface perpendicular to the surface
alpha is the angular acceleration vector
omega the angular velocity vector
theta is the angular position vector
L is the moment of inertia
tau is the torque
So, take your time solving this system of quations for the positional coordinate-vector and the angular vector. Your method of solution should be numerical using finite differentials. Write it up in a neat little program, adding the possibility to control the sphere with a gamepad, mouse or keyboard. Please add some scenery and other competing spheres, the four elements of nature, a racing track smoothed with splines and whatnot other stuff. And yes, take care to avoid numerical instabilities in the solution.
Take your time and hand in the solution by the end of the class. I'll just stand here and sip my coffee until you have completed the assignment. You may begin now.


Very nice beta! the controls are a tad sensitive, but otherwise this is great!
Thanks! Did you use mouse, keyboard or gamepad?