In this tutorial, I will provide a brief overview of proportional navigation family of guidance laws, but more importantly, we will go over some sample code so you get straight to trying it out in your own game. This tutorial (and accompanying demonstration video) is written using World in Conflict MW Mod. Sample codes are written in Python for MW Mod's FLINT Missile System.
History of Proportional Navigation (PN)
PN is the foundation of modern homing guidance in virtually every guided missiles in use today. The theory of PN was developed by the US Navy during World War II as desperate measures were needed to protect their ships from Japanese kamikaze attacks, and gun-based defense systems (even automated fire director controlled guns) simply did not have the range to take out the target at a safe distance, and easily became overwhelmed by saturation. Automatic homing missiles were urgently needed to defend ships at sea.
Although theory of PN was apparently known by the Germans during WW II, no applications were reported and the war shortly ended thereafter. The US Navy's experimental Lark missile was the first to implement PN, soon followed by Sparrow and the venerable AIM-9 Sidewinder after the war.
PN is cheap to implement and had demonstrated to provide effective homing guidance-- It is because PN does not require geometry information such as range to target and target speed (though it can also benefit from it), making it ideal to implement on simpler "range-denied" missiles, such as passively heat-seeking IR missiles and semi-active laser homing variants. Not only that, the theory of using Line of Sight (LOS) information to develop collision course is such a powerful concept, that virtually every advanced guidance laws used today share their ancestry lineage back to PN. If you ever see people attempting to code so-called "advanced target homing" missiles in games using quadratic equations and trigonometry, you can clearly see that they're reinventing the wheels and got some learning to do :-) PN totally laughs at, and beats out every other forms of homing guidance used by games, which integrate states by solving for what is essentially a high school geometry.
Understanding Theory of PN
PN works on the principle of "Constant Bearing Decreasing Range" (CBDR), where when two objects are heading in the same direction with no change in Line of Sight (bearing) angle, objects *will* collide. Line of Sight (LOS) is an imaginary sight-line between you and the target; when target is moving from left to right in your field of view, it is said that the LOS angle is changing from left to right. If however, you were to also run from left to right and accelerate appropriately to keep the target centered in your field of view, it is then said the rate at which LOS angle is changing (LOS rotation rate) is zero ("null"). Continuing to run with LOS rate maintained at zero will result in intercept and "lead to pursuit" collision with the object you're chasing.
Mathematically, PN is stated as follows:
Commanded Acceleration = N * Vc * LOS_Rate
N = Unitless navigation gain (constant) -- between 3 to 5
Vc = Closing Velocity (or "range closing rate")
LOS_Rate = LOS Rotation Rate
To describe this along a two-dimensional missile-target engagement geometry:
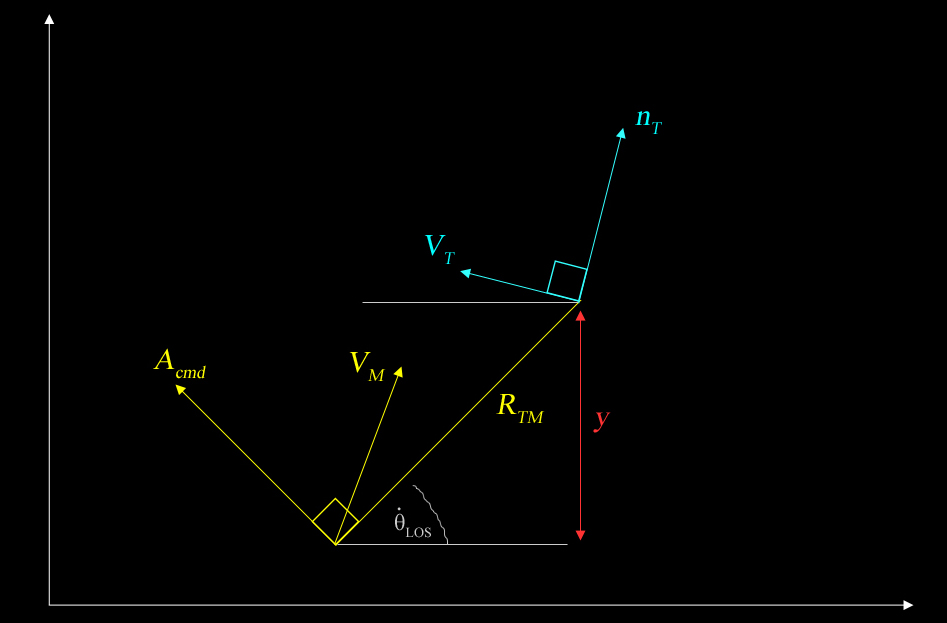
When working with PN, it is important to understand that missile's acceleration is commanded (Acmd) normal to (aka perpendicular to) the LOS, and proportional to the LOS rotation rate. LOS as stated earlier, is the sight-line between missile and the target, which would be "Rtm" line in the above diagram. LOS rotation rate is the angular rate at which the LOS line changes -- denoted by the over-dot theta "LOS" grey angle in the diagram above.
Prerequisites
Before we get started, we first assume that you already have very basic knowledge in implementation of homing missiles in game. If you are this far, you probably know that in order for your game physics to work, you need some sort of integration scheme (i.e Euler, Verlet, Runge-Kutta 4, etc) that provides step-by-step numerical integration at every frame. FLINT missile system in WiC MW uses Velocity-Verlet, but essentially, what it all comes down to is simple: you step forward one step (or frame) at a time and solve for your states. If you need help with game physics and integrators, check out Gafferongames.com
Implementing PN in Game
Now, to implement PN, we need to fill in the blanks from the above equation "An = N * Vc * LOS_Rate." Let's discuss how to obtain the individual input variables to calculate our required lateral acceleration (latax).
1. Obtaining the LOS Rotation Rate (LOS_Rate)
As explained above; LOS Rotation Rate is the rate at which target is crossing your field of view, or more exactly, the rate at which sight-line angle is changing.
Obtaining LOS_Rate is easy, especially in game environment. In real life, the missile seeker sits on a gimbaled gyro -- the seeker rotates in the gyro to keep the target locked on; the rate at which it rotates is your LOS rate. In real life, engineers have to contend with seeker noise contamination, but in games, we're essentially working in a noise-free environment.
First, you need to obtain the directional vector between the missile and the target (remember "Rtm" in the above diagram?) -- this is your LOS:
RTM_new = math.Vector3( targetPosition ) - math.Vector3( missilePosition )You will measure and record LOS at every frame; you need to now get the difference between the new RTM (RTM_new) you just measured, and the LOS obtained from the previous frame (RTM_old) -- this is your change in LOS (LOS_Delta).
RTM_new.Normalize()
RTM_old.Normalize()
LOS_Delta = ( RTM_new - RTM_old )
LOS_Rate = LOS_Delta.VectorLength()2. Closing Velocity (Vc)
Closing Velocity (Vc) is the rate at which the missile and the target are closing onto one another. In other words, as the missile is traveling toward its target, it gets closer to the target, no? So, the rate at which our missile is closing the distance to its target is called the "range closing rate" or simply "closing velocity." This range rate is mathematically defined as follows:
Vc = -Rtm_overdot
-Rtm_overdot = Negative rate of change of the distance from the missile to the target.Now, this raises a curious question: How do you obtain 'range rate' on a passive heat-seeking missiles that have no radar to measure distance? Well, you guesstimate it (lol) -- that's what the early rudimentary version of Sidewinder in 1953 did. Doesn't work very well against accelerating or maneuvering targets, but it was effective enough for what was world's first PN heat-seeking missile. In modern versions like the AIM-9L, AIM-9X, Stinger etc, you have computation power available in the seeker to "process" the intensity of IR or the image it sees. As IR signature gets closer, it gets more intense -- the rate of intensity change is your range closing rate.
On radar guided missiles, including semi-active homers like the original Sparrow missile, you have better luck! On a radio-frequency based sensor, the seeker can observe Doppler frequency of the target return to calculate the rate at which the missile is closing onto its target. Doppler effect is quite measurable on wavelengths as you get closer or away from the target. Negative rate of change in Doppler frequency is the closing velocity.
Anyway, now let's back to our in-game code. Recall from earlier that we derived our LOS_Rate in vector space as the difference between the current frame's missile-target vector (RTM_new) and the previous frame's missile-target vector (RTM_old). The length of the vector for this difference is denoted as LOS_Rate above. Well, just so it happens, as our missile is closing onto the target, RTM_new is shorter than RTM_old! So LOS_Rate length itself is a rate of change in missile-target distance. Then, conversely speaking, the negative rate of this distance change is our range closing rate, aka the closing velocity:
Vc = -LOS_Rate
3. Navigation Gain (N)
Navigation gain (or navigation constant) is a designer-chosen unitless variable usually in the range of 3 to 5. Higher the N, the faster your missile will null out heading errors. Generally, it is recommended for N to stay between 3 to 5. FLINT missiles in WiC MW use N of 3; most missiles in real-life use 3 as well.
4. Augmented Proportional Navigation (APN)
When implementing PN, it is best practice to focus on target's acceleration normal to LOS'-- we're using a missile to hit a moving target after all. What does 'acceleration normal to LOS' mean exactly? Well, as the missile is homing onto the target, the target would most likely move laterally, or 'perpendicular to' along the LOS sight-line (crossing target would present the most movement normal to LOS).
The reality is that, often times the target is not moving at a constant velocity -- it changes directions, or it slows down or accelerates. You also have upward sensible acceleration of 1 G even for non-maneuvering targets if you're simulating gravity.
To account for these factors, you add a term to our PN formula by adding "(N * Nt ) / 2":
Commanded Acceleration = N * Vc * LOS_Rate + ( N * Nt ) / 2
Nt = Target acceleration (estimated) normal to LOS
Even for targets that do not maneuver, the target's one-g sensible acceleration is multiplied by N/2, producing a more efficient intercept.
Putting it all together - Sample Code
Below is a sample FLINT missile system code for FIM-92 Stinger heat-seeking missile, written in Python. It is the simplest missile in game to employ augmented PN, as it's a passive heat-seeking missile.
def GCFLINT_Lib_APN( msl_pos, tgt_pos, msl_pos_previous, tgt_pos_previous, latax, N = None, Nt = None ):
"""
Augmented Proportional Navigation (APN)
A_cmd = N * Vc * LOS_Rate + N * Nt / 2
msl_pos: Missile's new position this frame.
tgt_ps: Target's new position this frame.
msl_pos_previous: Mutable object for missile's position previous frame.
tgt_pos_previous: Mutable object for target's position previous frame.
Set these objects to "0" during first time initialization, as we haven't
yet started recording previous positions yet.
latax: Mutable object for returning guidance command.
N: (float, optional) Navigation gain (3.0 to 5.0)
Nt: (float, optional) Target acceleration amount normal to LOS
"""
import wic.common.math as math
from predictorFCS_flint_includes import *
from predictorFCS_EXFLINT import *
if N is None:
# navigation constant
N = 3.0
else isinstance(N, float) is not True:
raise TypeError("N must be float")
if Nt is None:
# one-g sensible acceleration
Nt = 9.8 * EXFLINT_TICKTOCK
else isinstance(Nt, float) is not True:
raise TypeError("Nt must be float")
if msl_pos_previous is not 0 and tgt_pos_previous is not 0:
# Get msl-target distances of previous frame and new frame (Rtm)
RTM_old = ( math.Vector3( tgt_pos_previous ) - msl_pos_previous )
RTM_new = ( math.Vector3( tgt_pos ) - msl_pos )
# normalize RTM vectors
RTM_new.NormalizeSafe()
RTM_old.NormalizeSafe()
if RTM_old.Length() is 0:
LOS_Delta = math.Vector3( 0, 0, 0 )
LOS_Rate = 0.0
else:
LOS_Delta = math.Vector3( RTM_new ) - RTM_old
LOS_Rate = LOS_Delta.VectorLength()
# range closing rate
Vc = -LOS_Rate
# Now, calculate the final lateral acceleration required for our missile
# to home into our target.
latax = RTM_new * N * Vc * LOS_Rate + LOS_Delta * Nt * ( 0.5 * N )
# Update mutable position objects so we can integrate forward to next frame.
msl_pos_previous = math.Vector3( msl_pos )
tgt_pos_previous = math.Vector3( tgt_pos )
# my job is done, it's now up to EXFLINT.Integrate() to steer the missile.
return True
Video Demonstration and Wrapping it All Together
The augmented PN (APN) formula above should always be used for any moving targets-- even non-maneuvering aircraft should have upward one-g sensible acceleration in a proper simulation environment, necessitating the need for APN.
The advantage of using APN guidance as compared to classic PN is that the commanded lateral acceleration (latax) is initially high but falls as the missile approaches the maneuvering target. Watch the YouTube video accompanying this blog post very closely-- you'll see that APN guided missile initially makes very violent maneuver to snap itself onto the collision path, then only minor adjustments are made just prior to missile impact. This is how optimal PN is implemented in the real world and how it should be done in realistic combat simulation games.
In the next (near future) tutorial, we will go over advanced guidance laws using theories of optimal control, which are derivatives of PN with more engagement information fed in, such as estimated time-to-intercept; and missile-target range. Feel free to message me on ModDB or YouTube if you have any questions or comments about implementing PN in your game environment.
YouTube HD Link: youtu.be/Osb7anMm1AY
Is that okay with you if I link your article on /r/gamedev ?
Absolutely, please feel free!
Hi! Please help me to understand realization PN in 3D space.
Bro, I really really love your post!! can you give me some references for all the approaches that you have developed? please!!
Thanks for sharing such amazing info.
Love this post
Hey blahdy21,
I'm building missile guidance code in Unity as a personal project of mine. I have managed to nail down guidance in 3D in space by calculating the exact impact point. I have however found that this approach doesn't work on a planetary level with gravity and drag. I then stumbled upon your videos on APN and your blog.
I have been trying to implement APN for a while now but I can't seem to get it right. The point where I get stuck is what to do with the calculated required lateral acceleration, I have found a bazillion ways to calculate that acceleration in papers and in your videos but I don't know what to do with it. My main guess was:
Steering angle = Asin(required lateral acceleration / total missile acceleration)
But this just results in the missile going in a straight line because it gets in a feedback loop where it oscillates over a certain value. Could you maybe show or explain how you steer the missile with the calculated Latax?
Thanks in advance,
Boostback
Hey boostpack,
If you apply an acceleration NORMAL to a particle's velocity, you would get a turning motion, where the radius is defined as r = v^2 / a; the keyword here is NORMAL, and that's exactly how to use it: it is applied normal to the direction of motion and the axis of rotation. this is like a centripedal acceleration, and it will not add any tangential velocity to your particle(your missile wouldn't speed up to put it simply, although it does accelerate in the radial transverse coordinate system, strictly speaking) ideally. which is most likely not going to happen, and that's because the ''normality'' is determined by the precision of the numbers you are working with, because if the angle is not perfectly 90 degrees, it will result in accelerations along the direction of motion.
To answer your question in one sentence, you add the acceleration to your missile's acceleration! :)
Feel free to correct any mistakes i may have made or ask me more, i would be glad to help out!
Alex
Hey Xenonalex,
I think I figured out where I went wrong. I think with the method described here you first apply acceleration, get velocity from there and then get the rocket direction from the velocity direction. I approached things completely differently, I am simulating the missile as a real thing with only one acceleration source (It's main engine) and then working out which direction it needs to turn to hit it's target. Below is my working code for Proportional Navigation:Vector3 LOS = target.transform.position - transform.position;
Vector3 LOSGain = LOS.normalized - prevLOS.normalized;
float LOSAng = Vector3.Angle(transform.forward, LOS);
Vector3 perpVec = Vector3.Cross(LOS.normalized, LOSGain.normalized); //perpVec is perpindicular to both the LOS and the LOS change
float rotation_Speed = Mathf.Clamp(Mathf.Abs(LOSGain.magnitude * N), 0, maxAngCorr); //rotation_Speed = Omega * N (Clamped to maximum rotation speed)
if (LOSAng < 60)
{
Quaternion rot = Quaternion.AngleAxis(rotationSpeed, perpVec.normalized); // rotate with rotationSpeed around perpVec axis.
transform.rotation *= rot;
}
else
{
Vector3 newDirection = Vector3.RotateTowards(transform.forward, LOS, maxAngCorr*Mathf.Deg2Rad, 0.0f); //Turn towards target at maximum rotation speed
transform.rotation =
Quaternion.LookRotation(newDirection);
}
prevLOS = LOS;
Thanks for the help!
I'm very confused with both this example and the original code; why is LOS_delta/LOSGain the subtraction of these vectors instead of the dot or cross product to get the angle?
You subtract these vectors to get the change in line of sight. If you subtract two vectors you get the vector connecting their endpoints. This is the one we want because it encodes both how much the line of sight changed (in it's length) and in what direction (the direction of the vector). This vector is the direction you want to rotate in, with a rotational speed proportional to it's length. You do the rotation by taking the cross product between the current LOS and the change in LOS (which gives a vector perpendicular to both of them) and taking this as a rotation axis.
Small note: To get the difference between the vectors for these purposes you need to normalise them. The LOS vector is in world space and if you don't normalise them before subtracting them it would also encode the missile closing speed to its target.
> With rotational speed proportional to its length
My confusion is with this. Everywhere else, I've read that it's supposed to be proportional to the change in line of sight angle, not change of (normalized) line of sight vectors.
The length of the difference of the Line of sight vectors encodes this information. In others words, the length of the vector obtained by substraction is directly proportional with the change in line of sight angle. By encoding it in a vector you get all the information you would get from the change in line of sight angle *plus* the directional information for free.
+1
The length of the difference of the Line of sight vectors encodes this information. In others words, the length of the vector obtained by substraction is directly proportional with the change in line of sight angle. By encoding it in a vector you get all the information you would get from the change in line of sight angle *plus* the directional information for free.
Wouldn't the length of the difference be 2*cos(theta/2)? It's not exactly proportional. Is it just close enough for the angles involved?
The cross product already has both encoded as well (magnitude is the sine of the angle)
I see, anything close to proportional works though I guess. It isn't an exact science for what I need it for (and I don't think it is an exact science in general, that would be optimal control). About the cross product, If I understand it correctly that could also work and may give you an exact proportional relationship. I haven't done the math for this, everything is based on intuition.
Still one of the best and only posts out there on gamedev APN implementation. Really appreciate you putting this together years back. Cheers!
Thanks!
How to calculate Nt? Can you please write formula to calculate it
nT is generally target acceleration normal to your line of sight. You could express this in G loading/force or difference in target's velocity measured relative to missile point of view.
At very minimum, if your missile lacks capability to measure nT (range denied, passive seeker, etc), you should use 1.0 for nT as it represents 1G against acceleration by gravity in baseline simulation.
Hello blahdy, so i have applied the formula acquired Acmd it increases when missile is off intercept course and decreases when it is.
But i am playing a different game SR2 and i made the actual missile hardware with fins and pitch,yaw control with 45 degree actuators that have -1,1 inputs and so i don't know how Acmd can help me i need -1,1 commands sent to the actuators but i just don't know how to switch the acceleration command to a controlled pitch,yaw command.
The good thing is this game gives you all you need interms of target information and maths
Note: in SR2 you can make a custom anything then put a command chip with custom coding on it.
Simplerockets.com
This the missile system i made.
Turns out 2/180×90-1 as basic as it is was my solution in steering actuators, and it works very well.
Hey, I'm trying to implement this in Unity C#, and I started off by translating your code from Python to C#:
public class Missile : MonoBehaviour
{
[SerializeField] Transform debugObj;
[SerializeField] Transform target;
[SerializeField] float acceleration;
Rigidbody rb;
Vector3 missilePos;
Vector3 missilePosPrev;
Vector3 targetPos;
Vector3 targetPosPrev;
Vector3 latax;
[SerializeField] float N;
[SerializeField] float Nt;
Vector3 LOS_Delta;
float LOS_Rate;
float closingRate;
void Start()
{
rb = GetComponent<Rigidbody>();
rb.velocity = transform.up * 100; //Adding velocity once at the start, not necessary
}
void FixedUpdate()
{
//Implementation starts here...
missilePos = transform.position;
targetPos = target.position;
if(missilePosPrev != null || targetPosPrev != null)
{
var RTM_old = targetPosPrev - missilePosPrev;
var RTM_new = targetPos - missilePos;
RTM_old.Normalize();
RTM_new.Normalize();
if(RTM_old.magnitude == 0)
{
LOS_Delta = Vector3.zero;
LOS_Rate = 0f;
}
else
{
LOS_Delta = RTM_new - RTM_old;
LOS_Rate = LOS_Delta.magnitude;
}
closingRate = -LOS_Rate;
latax = RTM_new * N * closingRate * LOS_Rate + LOS_Delta * Nt * (0.5f * N);
}
missilePosPrev = missilePos;
targetPosPrev = targetPos;
//... and ends here
rb.AddForce(latax.normalized * acceleration); //Accelerating in the direction of latax
//Debugging, can also be ignored
Debug.DrawRay(transform.position, latax.normalized * 10, Color.red);
Debug.Log(rb.velocity.magnitude);
}
//Detecting Collisions, ignore this
private void OnTriggerEnter(Collider other)
{
rb.velocity = Vector3.zero;
rb.isKinematic = true;
}
}
Im struggling to understand a few things:
- The way I understand it, nT is always normal to the LOS, without ever changing the actual speed of the target (resulting in a circular motion). However due to my lack of understanding, Im keeping nT at 1 currently. Ive read in a comment by Xenonalex that target acceleration in for example the same direction as its velocity Vector should simply be added to the missiles' acceleration. How exactly would I do that? And how can I use nT correctly?
- Another problem I have is that I would like my missile to continuously accelerate, however with this current implementation, it only accelerates up to a certain speed, and then constantly attempts to maintain that speed by negating latax. For example, if it starts with a velocity of 20 in a random direction, it will accelerate while adjusting its velocity vector to face towards the intercept point, and then stops accelerating. How could I make it continously accelerate while still maintaining a straight flight path?
Other than this, I really love all of the information youve provided, and it remains the best documeentation on the subject available online!